江苏省姜堰市初二下学期期中考试数学卷
如图2,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为
| A.20 | B.18 | C.16 | D.15 |
如图,⊙O的弦AB=6,M是AB上任意一点,且OM最小值为4,⊙O的半径为
| A.5 | B.4 | C.3 | D.2 |
动物园的门票售价:成人票每张50元,儿童票每张30元.某日动物园售出门票700张,共得29000元.设儿童票售出x张,依题意可列出的一元一次方程是
| A.30x+50(700-x)=29000 | B.50x+30(700-x)=29000 |
| C.30x+50(700+x)=29000 | D.50x+30(700+x)="29000" |
如图,一只蚂蚁从 点出发,沿着扇形
点出发,沿着扇形 的边缘匀速爬行一周,设蚂蚁的运动时间为
的边缘匀速爬行一周,设蚂蚁的运动时间为 ,蚂蚁到
,蚂蚁到 点的距离为
点的距离为 ,则
,则 关于
关于 的函数图象大致为
的函数图象大致为
如图,在矩形ABCD中,AB=11cm,BC=6cm,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A’,D’处,则整个阴影部分图形的周长为
A.17cm B.34cm C.28cm D.66cm
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①a>0.
②该函数的图象关于直线 对称.
对称.
③当 时,函数y的值都等于0.
时,函数y的值都等于0.
其中正确结论的个数是
| A.3 | B.2 | C.1 | D.0 |
点A1、 A2、 A3、 …、 An(n为正整数)都在数轴上.点A1在原点O的左边,且A1O=1;点A2在点A1的右边,且A2A1=2;点A3在点A2的左边,且A3A2=3;点A4在点A3的右边,且A4A3=4;……,依照上述规律,点A2006、 A2007所表示的数分别为
| A.2006、-2007 | B.-2006、 2007 |
| C.1003、-1004 | D.1003、 -1003 |
甲、乙两人进行跳远训练时,在相同条件下各跳10次的平均成绩相同,若甲的方差为0.3,乙的方差为0.4,则甲、乙两人跳远成绩较为稳定的是_______.
如图,将△OAB绕点0按逆时针方面旋转至△0′A′B′,使点B恰好落在边A′B′上.已知AB=10cm,BB′=3cm,则A′B的长是 cm.

如图,扇形的半径为6,圆心角 为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为________.
为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为________.
如图,在直角坐标系中,已知点 ,
, ,对△
,对△ 连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 .
连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 .
如图所示,正方形网格中, 为格点三角形(即三角形的顶点都在格点上).
为格点三角形(即三角形的顶点都在格点上).
(1)把 沿
沿 方向平移后,点
方向平移后,点 移到点
移到点 ,在网格中画出平移后得到的
,在网格中画出平移后得到的 ;
;
(2)把 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 ,在网格中画出旋转后的
,在网格中画出旋转后的 ;
;
(3)如果网格中小正方形的边长为1,求点 经过(1)、(2)变换的路径总长.
经过(1)、(2)变换的路径总长.
有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的 ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字
,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字 记作一次函数表达式中的
记作一次函数表达式中的 .
.
(1)写出 为负数的概率;
为负数的概率;
(2)求一次函数 的图象经过二、三、四象限的概率.(用树状图或列表法求解)
的图象经过二、三、四象限的概率.(用树状图或列表法求解)
如图,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1km,B村到公路l的距离BD=2km,B村在A村的南偏东45°方向上.
(1)求出A,B两村之间的距离;
(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置(不写作法,保留清晰的作图痕迹).
|
|
如图,△ABC是等边三角形,CE是外角平分线, 点D在AC上,连结BD并延长与CE交于点E.

(1)求证:
 △ABD∽△CED.
△ABD∽△CED.(2)若AB=6,AD=2CD,求BE的长.
已知:如图,正比例函数 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点

(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?
(3) 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中 过点
过点 作直线
作直线 轴,交
轴,交 轴于点
轴于点 ;过点
;过点 作直线
作直线
 轴交
轴交 轴于点
轴于点 ,交直线
,交直线 于点
于点 .当四边形
.当四边形 的面积为6时,请判断线段
的面积为6时,请判断线段 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60º.

(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从A 点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动
点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动
 ,设运动时间为
,设运动时间为 ,连结E
,连结E F,当
F,当 为何值时,△BEF为直角三角形.
为何值时,△BEF为直角三角形.
如图所示,已知在直角梯形 中,
中, 轴于点
轴于点 .动点
.动点 从
从 点出发,沿
点出发,沿 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过 点作
点作 垂直于直线
垂直于直线 ,垂足为
,垂足为 .设
.设 点移动的时间为
点移动的时间为 秒(
秒( ),
), 与直角梯形
与直角梯形 重叠部分的面积为
重叠部分的面积为 .
.
(1)求经过 三点的抛物线解析式;
三点的抛物线解析式;
(2)求 与
与 的函数关系式;
的函数关系式;
(3)将 绕着点
绕着点 顺时针旋转
顺时针旋转 ,是否存在
,是否存在 ,使得
,使得 的顶点
的顶点 或
或 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
下列运算中,正确的是 ( )
| A.3x2+2x3=5x5 | B.x3·x3="x6" | C.(x2)3=x5 | D.(x+y)2=x2+y2 |
如果a>b,则下列不等式一定成立的是( )
| A.1-a<1-b | B.–a>-b | C.ac2 >bc2 | D.a-2<b-2 |
若a>b,则下列各式中一定成立的是( )
| A.3a<3b | B.ac>bc | C.-a<-b | D.a-1<b-1 |
若分式x+y/x-2y中的x、y的值都变为原来的
3倍,则此分式的值( )
| A.不变 | B.是原来的3倍 | C.是原来的 |
D.是原来的 |
点M (-2,3)在曲线 上,则下列点一定在该曲线上的是( )
上,则下列点一定在该曲线上的是( )
| A.(2,3 ) | B.(-2,-3 ) | C.(3,-2 ) | D.(3,2) |
已知反比例函数 ,下列结论不正确的是( )
,下列结论不正确的是( )
| A.图象经过点(1,1) | B.图象在第一、三象限 |
C.当 时, 时, |
D.当 时, 时, 随着 随着 的增大而增大 的增大而增大 |
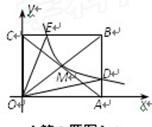
如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为( )
|
是否存在这样的整数m,使方程组 的解x、y为非负数,若存在,求m的取值?若不存在,则说明理由.
的解x、y为非负数,若存在,求m的取值?若不存在,则说明理由.
如图:已知直线y= 与双曲线y=
与双曲线y= 交于A、B两点,且点A的横坐标为4
交于A、B两点,且点A的横坐标为4
⑴求k的值;
⑵若双曲线y= 上的一点C的纵坐标为8,求△AOC的面积?
上的一点C的纵坐标为8,求△AOC的面积?
4个男生和6个女生到图书馆参加装订杂志的义务劳动.管理员要求每人必须独立装订.而且每个男生的装订数是每个女生的2倍.在装订过程中发现.女生们装订的总数肯定超过30本.男、女生们装订的总数肯定不到98本.问:男、女生平均每人装订多少本?
进入防汛期后,某市对河堤进行了加固.该市水利工程公司在河堤加固的工程中出色完成了任务.这是记者与工程指挥员的一段对话:
如图,已知 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求方程 的解(请直接写出答案);
的解(请直接写出答案);
(3)设D(x,0)是x轴上原点左侧的一点,且满足 ,求x的取值范围.
,求x的取值范围.
如图所示的矩形包书纸中,虚线是折痕,阴影是裁剪掉的部分,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.
(1)设课本的长为a cm,宽为b cm,厚为c cm,如果按如图所示的包书方式,将封面和封底各折进去3cm,用含a,b,c的代数式,分别表示满足要求的矩形包书纸的长与宽;
(2)现有一本长为19cm,宽为16cm,厚为6cm的字典,你能用一张长为43cm,宽为26cm的矩形 纸,按图所示的方法包好这本字典,并使折叠进去的宽度不小于3cm吗?请说明理由.
纸,按图所示的方法包好这本字典,并使折叠进去的宽度不小于3cm吗?请说明理由.




 结果是
结果是 )是关于x的方程
)是关于x的方程 的根,则m+n的值为
的根,则m+n的值为  .
.
 的值为0,则m的值为 ( )
的值为0,则m的值为 ( ) 和
和 都经过点
都经过点 ,则不等式
,则不等式 的解集为
的解集为




 中,自变量
中,自变量 的取值范围是 .
的取值范围是 .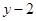 与
与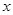 成反比例,当
成反比例,当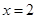 时,
时,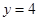 ,则当
,则当 时,
时,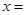 .
. 的最简公分母是____________.
的最简公分母是____________. 10g,表明了这罐八宝粥的净含量
10g,表明了这罐八宝粥的净含量 的范围是 .
的范围是 . 在第二象限内,且
在第二象限内,且 为整数,则P点坐标为 .
为整数,则P点坐标为 . 的分式方程
的分式方程 无解,则
无解,则 的值为 .
的值为 .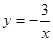 的图象上有两个点(-2,
的图象上有两个点(-2,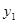 ),(-1,
),(-1,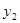 ),则函数值
),则函数值 中,若未知数x、y满足x+y>0,则m的取值范围是 .
中,若未知数x、y满足x+y>0,则m的取值范围是 . 的解集是
的解集是 ,则a应满足的条件是______.
,则a应满足的条件是______.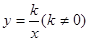 与
与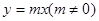 图象的一个交点坐标为
图象的一个交点坐标为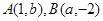 ,则
,则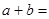 。
。

 选一个使原代数式有意义的数代入求值.
选一个使原代数式有意义的数代入求值. 与AB,BC交于点M,N.
与AB,BC交于点M,N.
 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上; ,请直接写出m的取值范围.
,请直接写出m的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号