2008年全国统一高考文科数学试卷(上海卷)
已知总体的各个体的值由小到大依次为2,3,3,7, ,12,13.7,18.3,20,且总体的中位数为10.5,若要使该总体的方差最小,则 的取值分别是.
来源:2008年高考上海卷理科数学试题
如图,在平面直角坐标系中, 是一个与 轴的正半轴、 轴的正半轴分别相切于点 、 的定圆所围成区域(含边界), 、 、 、 是该圆的四等分点,若点 、 满足 且 ,则称 优于 ,如果 中的点 满足:不存在 中的其它点优于 ,那么所有这样的点 组成的集合是劣弧( )

| A. |
|
B. | C. | D. |
来源:2008年高考上海卷理科数学试题
给定空间中的直线 及平面 .条件"直线 与平面 内两条相交直线都垂直"是"直线 与平面 垂直"的()
| A. | 充分非必要条件 | B. | 必要非充分条件 |
| C. | 充要条件 | D. | 既非充分又非必要条件 |
来源:2008年高考上海卷数学文试题
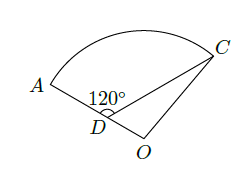
如图,某住宅小区的平面图呈扇形
.小区的两个出入口设置在点
及点
处,小区里有两条笔直的小路
,且拐弯处的转角为
.已知某人从
沿  走到
用了10分钟,从
沿
走到
用了6分钟.若此人步行的速度为每分钟50米,求该扇形的半径
的长(精确到1米).
走到
用了10分钟,从
沿
走到
用了6分钟.若此人步行的速度为每分钟50米,求该扇形的半径
的长(精确到1米).
来源:2008年高考上海卷数学文试题
已知双曲线
.
(1)求双曲线
的渐近线方程;
(2)已知点M的坐标为
.设
是双曲线
上的点,
是点
关于原点的对称点.记
.求
的取值范围;
(3)已知点
的坐标分别为
,
为双曲线
上在第一象限内的点.记
为经过原点与点
的直线,
为
截直线
所得线段的长.试将
表示为直线
的斜率k的函数.
来源:2008年高考上海卷数学文试题
 是椭圆
上的点.若
是椭圆的两个焦点,则
等于()
是椭圆
上的点.若
是椭圆的两个焦点,则
等于() 粤公网安备 44130202000953号
粤公网安备 44130202000953号