2012年全国统一高考理科数学试卷(北京卷)
设不等式 表示的平面区域为 ,在区域 内随机取一个点,则此点到坐标原点的距离大于 的是()
| A. | B. | C. | D. |
设 ," "是"复数 是纯虚数"的()
| A. | 充分而不必要条件 | B. | 必要而不充分条件 |
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
从0,2中选一个数字.从1,3,5中选两个数字,组成无重复数字的三位数.其中奇数的个数为()
| A. | 24 | B. | 18 | C. | 12 | D. | 6 |
某棵果树前 年的总产量 与 之间的关系如图所示,从目前记录的结果看,前 年的年平均产量最高, 的值为( )
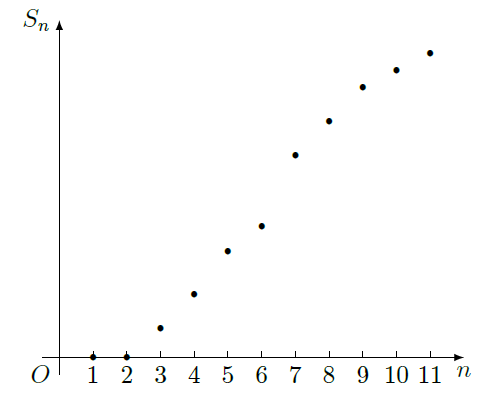
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
在直角坐标系中,直线过抛物线的焦点,且与该抛物线相交于、两点,其中点在轴上方.若直线的倾斜角为60º,则的面积是.为
如图1,在中,,,,分别是上的点,且,,将沿折起到的位置,使,如图2.
(1)求证:平面;
(2)若是的中点,求与平面所成角的大小;
(3)线段上是否存在点,使平面与平面垂直?说明理由
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱。为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| "厨余垃圾"箱 |
"可回收物"箱 |
"其他垃圾"箱 |
|
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在"厨余垃圾"箱、"可回收物"箱、"其他垃圾"箱的投放量分别为,其中,.当数据的方差最大时,写出的值(结论不要求证明),并求此时的值。
(注:,其中为数据的平均数)
已知函数,,.
(1)若曲线与曲线在它们的交点处具有公共切线,求的值
(2)当时,若函数的单调区间,并求其在区间上的最大值.
已知曲线
.
(1)若曲线
是焦点在x轴点上的椭圆,求
的取值范围;
(2)设
,曲线
与
轴的交点为
(点
位于点
的上方),直线
与曲线
交于不同的两点
,直线
与直线
交于点
.求证:
三点共线.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号