【八年级下册】全国重点高中提前招生单元过关(十八)
如图所示,在四边形 中, 分别是 的中点, 划分四边形所成的 个区域的面积分别为 ,那么,恒成立的关系式为( )

| A. |
|
B. |
|
C. |
|
D. |
|
已知菱形 的两条对角线 的乘积等于菱形的一条边长的平方,则菱形的一个钝角的大小是( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图所示, 中, ,正方形 的顶点 在 上,点 在 上,点 在 上,如果正方形 的面积是 面积的 ,那么 等于( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 分别是正方形 的边 的中点,要使中间阴影部分的小正方形的面积为 ,则大正方形的边长应该是( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图所示,四边形 的对角线 交于点 ,则四边形 的面积最小值是( )

| A. |
|
B. |
|
C. |
|
D. |
无法求出 |
已知一个正八边形最长的对角线等于 ,最短的对角线等于 ,则这个正八边形的面积等于( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,矩形 中,点 分别在边 上,点 在矩形 内.若 ,四边形 的面积为 ,则四边形 的面积为_____ .

如图所示, 的边 , ,I,Ⅱ,Ⅲ分别表示以 , , 为边的正方形,则图中三个阴影部分的面积之和的最大值是_____.

一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第 个正方形的边长是 ,则生长到第 次后,所得图形的面积是_____.

如图,四边形 是 的内接四边形。
(1)若 或 ,求证 ;
(2)若 ,问是否能推出 或 ?证明你的结论.

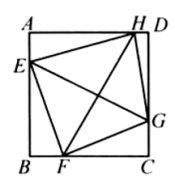
如图,四边形 是正方形 的内接四边形, 与 都是锐角,已知 ,四边形 的面积为 .求正方形 的面积.
问题探究:
(1)请你在图①中做一条直线,使它将矩形 分成面积相等的两部分;
(2)如图②,点 是矩形 内一点,请你在图②中过 点作一条直线,使它将矩形 分成面积相等的两部分.
问题解决:
(3)如图③,在平面直角坐标系 中,多边形 的顶点坐标分别是 .若直线 经过点 ,且将多边形 分割成面积相等的两部分,求直线 的函数表达式.

(1)如图①, 的面积是 ,点 是 的中点,连接 的面积是_____.
(2)如图②,四边形 的面积是 ,点 分别是一组对边 的中点,连接 ,则四边形 的面积是_____.
(3)如图③,点 分别是一组对边 上的点,且 ,若四边形 的面积是 ,连接 ,则四边形 的面积是_____.
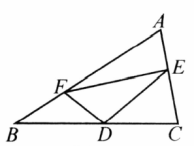
(4)如图④, 的面积是 ,点 从点 出发沿 以每秒 个单位长的速度向点 运动,点 从点 出发沿 以每秒 个单位长的速度向点 运动.点 分别从点 同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形 的面积的值是否随着时间 的变化而变化?若不变,请求出这个值;若变化,说明怎样变化的.




 粤公网安备 44130202000953号
粤公网安备 44130202000953号