2017年全国统一高考文科数学试卷（北京卷）

若集合 $A=\left\{x\right|﹣2＜x＜1\}$ ， $B=\left\{x\right|x\mathit{＜﹣}1或x＞3\}$ ，则 $A\cap B=$ （　　）

若复数 $\left(1﹣i\right)\left(a+i\right)$ 在复平面内对应的点在第二象限，则实数a的取值范围是（　　）

执行如图所示的程序框图，输出的S值为（　　）

若 $x，y$ 满足 $\{\begin{array}{c}x\le 3\\ x+y\ge 2\\ y\le x\end{array}$ ，则 $x+2y$ 的最大值为（　　）

已知函数 $f\left(x\right)=3^x﹣\left(\frac{1}{3}\right){}^x$ ， 则 $f\left(x\right)$ （　　）

设  $\stackrel{\to }{m}$ ， $\stackrel{\to }{n}$ 为非零向量，则"存在负数 $\lambda$ ，使得 $\stackrel{\to }{m}=\lambda \stackrel{\to }{n}$ "是 " $\stackrel{\to }{m}·\stackrel{\to }{n}<0$ "的（　　）

某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（　　）

根据有关资料，围棋状态空间复杂度的上限M约为 $3^{361}\mathit{ }$ ， 而可观测宇宙中普通物质的原子总数N约为 ${10}^{80}\mathit{ }$ ， 则下列各数中与 $\frac{M}{N}$ 最接近的是（　　）

（参考数据： $\mathit{lg}3\approx 0.48$ ）

若双曲线 $x^2-\frac{y^2}{m}=1$的离心率为 $\sqrt{3}$ ，则实数 $m=$________．

若等差数列 $\left\{a_n\right\}$和等比数列 $\left\{b_n\right\}$满足 $a_1=b_1=﹣1$， $a_4=b_4=8$，则 $\frac{a_2}{b_2}$ =________．

在极坐标系中，点A在圆 ${\rho }^2﹣2\mathit{\rho cos\theta }﹣4\mathit{\rho sin\theta }+4=0$上，点P的坐标为 $（1，0）$，则 $\left|\mathit{AP}\right|$的最小值为________．

在平面直角坐标系 $\mathit{xOy}$中，角 $\alpha$与角 $\beta$均以 $\mathit{Ox}$为始边，它们的终边关于 $y$轴对称，若 $\mathit{sin\alpha }=\frac{1}{3}$ ，则 $\mathit{cos}（\alpha ﹣\beta ）=$________．

能够说明“设a，b，c是任意实数．若 $a＞b＞c$，则 $a+b＞c$”是假命题的一组整数a，b，c的值依次为________．

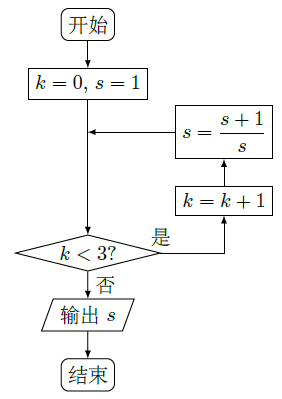
三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中 $A_i$的横、纵坐标分别为第 $i$名工人上午的工作时间和加工的零件数，点 $B_i$的横、纵坐标分别为第 $i$名工人下午的工作时间和加工的零件数， $i=1，2，3$．

①记 $Q_i$为第 $i$名工人在这一天中加工的零件总数，则 $Q_1$ ， $Q_2$， $Q_3$中最大的是________．

②记 $p_i$为第 $i$名工人在这一天中平均每小时加工的零件数，则 $p_1\mathit{ }$， $p_2$ ， $p_3$中最大的是________．

在 $△\mathit{ABC}$ 中， $\angle A=60°$ ， $c=\frac{3}{7}a$ ．

（1）求 $\mathit{sinC}$ 的值；

（2）若 $a=7$ ，求 $△\mathit{ABC}$ 的面积．

如图，在四棱锥 $P﹣\mathit{ABCD}$中，底面 $\mathit{ABCD}$为正方形，平面 $\mathit{PAD}\perp$平面 $\mathit{ABCD}$，点M在线段PB上， $\mathit{PD}\parallel$平面 $\mathit{MAC}$， $\mathit{PA}=\mathit{PD}=\sqrt{6}$ ， $\mathit{AB}=4$．

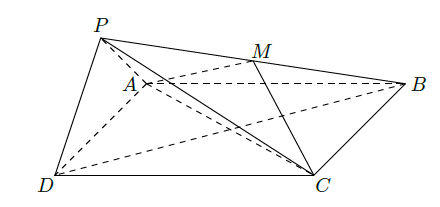
（1）求证：M为PB的中点；

（2）求二面角 $B﹣\mathit{PD}﹣A$的大小；

（3）求直线MC与平面BDP所成角的正弦值．

为了研究一种新药的疗效，选100名患者随机分成两组，每组各 $50$名，一组服药，另一组不服药．一段时间后，记录了两组患者的生理指标 $x$和 $y$的数据，并制成如图，其中“*”表示服药者，“+”表示未服药者．

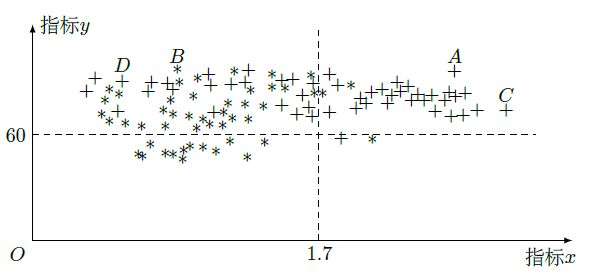
（1）从服药的50名患者中随机选出一人，求此人指标 $y$的值小于 $60$的概率；

（2）从图中A，B，C，D四人中随机选出两人，记 $\xi$为选出的两人中指标x的值大于1.7的人数，求 $\xi$的分布列和数学期望 $E（\xi ）$；

（3）试判断这100名患者中服药者指标 $y$数据的方差与未服药者指标y数据的方差的大小．（只需写出结论）

已知抛物线 $C：y^2=2\mathit{px}$ 过点 $P\left(1，1\right)$ ．过点 $\left(0，\frac{1}{2}\right)$ 作直线l与抛物线C交于不同的两点M，N，过点M作x轴的垂线分别与直线OP、ON交于点A，B，其中O为原点．

（1）求抛物线C的方程，并求其焦点坐标和准线方程；

（2）求证：A为线段BM的中点．

已知函数 $f\left(x\right)=e^x\mathit{cosx}﹣x$ ．

（1）求曲线 $y=f\left(x\right)$ 在点 $\left(\mathit{0}\mathit{，}\mathit{f}\left(\mathit{0}\right)\right)$ 处的切线方程；

（2）求函数 $f\left(x\right)$ 在区间 $\left[0，\frac{\pi }{2}\right]$ 上的最大值和最小值．

设 $\left\{a_n\right\}$和 $\left\{b_n\right\}$是两个等差数列，记 $c_n=\mathit{max}\{b_1﹣a_{1}n，b_2﹣a_{2}n，\dots ，b_n﹣a_{n}n\}（n=1，2，3，\dots ）$，其中 $\mathit{max}\{x_1\mathit{ }，x_2，\dots ，x_s\}$表示 $x_1\mathit{ }，x_2，$， …， $x_s$这s个数中最大的数．

（1）若 $a_n=n$， $b_n=2n﹣1$，求 $c_1\mathit{ }$， $c_2$， $c_3$的值，并证明{c_n}是等差数列；

（2）证明：或者对任意正数 $M$，存在正整数 $m$，当 $n\ge m$时， $\frac{c_n}{n}＞M$；或者存在正整数 $m$，使得 $c_m$ ， $c_{m+1}$ ， $c_{m+2}\mathit{ }$， …是等差数列．