2016年全国统一高考理科数学试卷(全国Ⅱ卷)
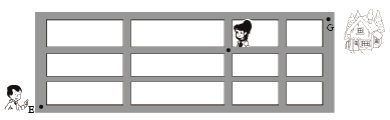
如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
| A. |
24 |
B. |
18 |
C. |
12 |
D. |
9 |
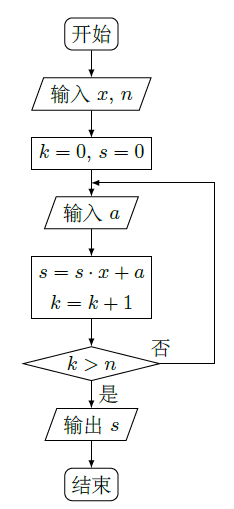
中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的 , ,依次输入的a为2,2,5,则输出的 ( )
| A. | 7 |
B. | 12 |
C. | 17 |
D. | 34 |
从区间 随机抽取2 n个数 , ,…, , , ,…, ,构成 n个数对 , ,…, ,其中两数的平方和小于1的数对共有 m个,则用随机模拟的方法得到的圆周率 的近似值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知 , 是双曲线 的左,右焦点,点 M在 E上, 与 轴垂直, ,则E的离心率为( )
| A. |
|
B. |
|
C. |
|
D. |
2 |
是两个平面, 是两条直线,有下列四个命题:
①如果 , , , 那么 .
②如果 , , 那么 .
③如果 , , 那么 .
④如果 , , 那么 所成的角和 所成的角相等.
其中正确的命题有________.(填写所有正确命题的编号)
有三张卡片,分别写有1和2,1和3,2和3。甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________。
为等差数列 的前n项和,且 记 ,其中 表示不超过x的最大整数,如 .
(1)求 ;
(2)求数列 的前1 000项和.
某险种的基本保费为 (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 |
0 |
1 |
2 |
3 |
4 |
5 |
保费 |
0.85a |
a |
1.25a |
1.5a |
1.75a |
2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 |
0 |
1 |
2 |
3 |
4 |
5 |
概率 |
0.30 |
0.15 |
0.20 |
0.20 |
0.10 |
0. 05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.
如图,菱形ABCD的对角线 与 交于点 , , ,点 分别在 上, , 交 于点 .将 沿 折到 的位置, .
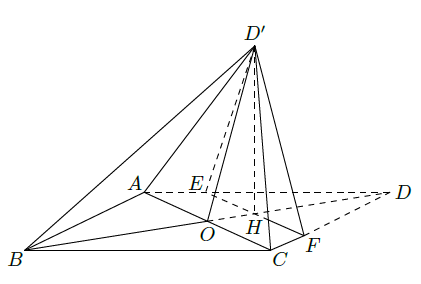
(1)证明: 平面 ;
(2)求二面角 的正弦值.
已知椭圆 的焦点在 轴上, A是 E的左顶点,斜率为 的直线交 E于 A, M两点,点 N在 E上, .
(1)当 , 时,求 的面积;
(2)当 时,求 k的取值范围.
(1)讨论函数 的单调性,并证明当 >0时,
(2)证明:当 时,函数 有最小值.设 的最小值为 ,求函数 的值域.
如图,在正方形 , 分别在边 上(不与端点重合),且 ,过D点作 , 垂足为F.
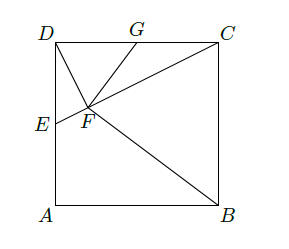
(1)证明: 四点共圆;
(2)若 ,E为DA的中点,求四边形BCGF的面积.
在直线坐标系 中,圆 C的方程为 .
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求 C的极坐标方程;
(2)直线 l的参数方程是 , l与 C交于 A、 B两点, ,求 l的斜率。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号