2018年浙江省嘉兴市（舟山市）中考数学试卷

下列几何体中，俯视图为三角形的是 $($　　 $)$

A．B．C．D．

2018年5月25日，中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日 $L2$点，它距离地球约 $1500000\mathit{km}$，数1500000用科学记数法表示为 $($　　 $)$

A． $15\times {10}^5$B． $1.5\times {10}^6$C． $0.15\times {10}^7$D． $1.5\times {10}^5$

2018年 $1~4$月我国新能源乘用车的月销量情况如图所示，则下列说法错误的是 $($　　 $)$

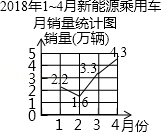
A．1月份销量为2.2万辆

B．从2月到3月的月销量增长最快

C．4月份销量比3月份增加了1万辆

D． $1~4$月新能源乘用车销量逐月增加

不等式 $1-x⩾2$的解在数轴上表示正确的是 $($　　 $)$

A．B．

C．D．

将一张正方形纸片按如图步骤①，②沿虚线对折两次，然后沿③中平行于底边的虚线剪去一个角，展开铺平后的图形是 $($　　 $)$

A．B．C．D．

用反证法证明时，假设结论“点在圆外”不成立，那么点与圆的位置关系只能是 $($　　 $)$

A．点在圆内B．点在圆上

C．点在圆心上D．点在圆上或圆内

欧几里得的《原本》记载，形如 $x^2+\mathit{ax}=b^2$的方程的图解法是：画 $\text{Rt}\Delta \text{ABC}$，使 $\angle \mathit{ACB}=90°$， $\mathit{BC}=\frac{a}{2}$， $\mathit{AC}=b$，再在斜边 $\mathit{AB}$上截取 $\mathit{BD}=\frac{a}{2}$．则该方程的一个正根是 $($　　 $)$

A． $\mathit{AC}$的长B． $\mathit{AD}$的长C． $\mathit{BC}$的长D． $\mathit{CD}$的长

用尺规在一个平行四边形内作菱形 $\mathit{ABCD}$，下列作法中错误的是 $($　　 $)$

A．B．

C．D．

如图，点 $C$在反比例函数 $y=\frac{k}{x}(x>0)$的图象上，过点 $C$的直线与 $x$轴， $y$轴分别交于点 $A$， $B$，且 $\mathit{AB}=\mathit{BC}$， $\mathit{\Delta AOB}$的面积为1，则 $k$的值为 $($　　 $)$

A．1B．2C．3D．4

某届世界杯的小组比赛规则：四个球队进行单循环比赛（每两队赛一场），胜一场得3分，平一场得1分，负一场得0分，某小组比赛结束后，甲、乙、丙、丁四队分别获得第一、二、三、四名，各队的总得分恰好是四个连续奇数，则与乙打平的球队是 $($　　 $)$

A．甲B．甲与丁C．丙D．丙与丁

分解因式： $m^2-3m=$　　．

如图，直线 $l_1//l_2//l_3$，直线 $\mathit{AC}$交 $l_1$， $l_2$， $l_3$于点 $A$， $B$， $C$；直线 $\mathit{DF}$交 $l_1$， $l_2$， $l_3$于点 $D$， $E$， $F$，已知 $\frac{\mathit{AB}}{\mathit{AC}}=\frac{1}{3}$，则 $\frac{\mathit{EF}}{\mathit{DE}}=$　　．

小明和小红玩抛硬币游戏，连续抛两次，小明说：“如果两次都是正面，那么你赢；如果两次是一正一反，则我赢．”小红赢的概率是　　，据此判断该游戏　　（填“公平”或“不公平” $)$．

如图，量角器的0度刻度线为 $\mathit{AB}$，将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点 $C$，直尺另一边交量角器于点 $A$， $D$，量得 $\mathit{AD}=10\mathit{cm}$，点 $D$在量角器上的读数为 $60°$，则该直尺的宽度为　　 $\mathit{cm}$．

甲、 乙两个机器人检测零件， 甲比乙每小时多检测 20 个， 甲检测 300 个比乙检测 200 个所用的时间少 $10\%$，若设甲每小时检测 $x$个， 则根据题意， 可列出方程：　　．

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AB}=4$， $\mathit{AD}=2$，点 $E$在 $\mathit{CD}$上， $\mathit{DE}=1$，点 $F$是边 $\mathit{AB}$上一动点，以 $\mathit{EF}$为斜边作 $\text{Rt}\Delta \text{EFP}$．若点 $P$在矩形 $\mathit{ABCD}$的边上，且这样的直角三角形恰好有两个，则 $\mathit{AF}$的值是　　．

（1）计算： $2(\sqrt{8}-1)+|-3|-{(\sqrt{3}-1)}^0$；

（2）化简并求值： $(\frac{a}{b}-\frac{b}{a})·\frac{\mathit{ab}}{a+b}$，其中 $a=1$， $b=2$．

用消元法解方程组 $\left\{\begin{array}{c}x-3y=5,①\\ 4x-3y=2\cdot ②\end{array}\right.$时，两位同学的解法如下：

解法一：

由① $-$②，得 $3x=3$．

解法二：

由②，得 $3x+(x-3y)=2$，③

把①代入③，得 $3x+5=2$．

（1）反思：上述两个解题过程中有无计算错误？若有误，请在错误处打“ $\times$ “．

（2）请选择一种你喜欢的方法，完成解答．

已知： 在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$， $D$为 $\mathit{AC}$的中点， $\mathit{DE}\perp \mathit{AB}$， $\mathit{DF}\perp \mathit{BC}$，垂足分别为点 $E$， $F$，且 $\mathit{DE}=\mathit{DF}$． 求证： $\mathit{\Delta ABC}$是等边三角形 ．

某厂为了检验甲、乙两车间生产的同一款新产品的合格情况（尺寸范围为 $176\mathit{mm}~185\mathit{mm}$的产品为合格），随机各抽取了20个样品进行检测，过程如下：

收集数据（单位： $\mathit{mm})$

甲车间：168，175，180，185，172，189，185，182，185，174，192，180，185，178，173，185，169，187，176，180．

乙车间：186，180，189，183，176，173，178，167，180，175，178，182，180，179，185，180，184，182，180，183．

整理数据：

分析数据：

应用数据：

（1）计算甲车间样品的合格率．

（2）估计乙车间生产的1000个该款新产品中合格产品有多少个？

（3）结合上述数据信息，请判断哪个车间生产的新产品更好，并说明理由．

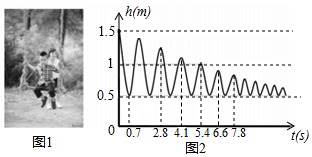
小红帮弟弟荡秋千（如图 $1)$，秋千离地面的高度 $ℎ\left(m\right)$与摆动时间 $t\left(s\right)$之间的关系如图2所示．

（1）根据函数的定义，请判断变量 $ℎ$是否为关于 $t$的函数？

（2）结合图象回答：

①当 $t=0.7s$时， $ℎ$的值是多少？并说明它的实际意义．

②秋千摆动第一个来回需多少时间？

如图1，滑动调节式遮阳伞的立柱 $\mathit{AC}$垂直于地面 $\mathit{AB}$， $P$为立柱上的滑动调节点，伞体的截面示意图为 $\mathit{\Delta PDE}$， $F$为 $\mathit{PD}$的中点， $\mathit{AC}=2.8m$， $\mathit{PD}=2m$， $\mathit{CF}=1m$， $\angle \mathit{DPE}=20°$，当点 $P$位于初始位置 $P_0$时，点 $D$与 $C$重合（图 $2)$．根据生活经验，当太阳光线与 $\mathit{PE}$垂直时，遮阳效果最佳．

（1）上午 $10:00$时，太阳光线与地面的夹角为 $65°$（图 $3)$，为使遮阳效果最佳，点 $P$需从 $P_0$上调多少距离？（结果精确到 $0.1m)$

（2）中午 $12:00$时，太阳光线与地面垂直（图 $4)$，为使遮阳效果最佳，点 $P$在（1）的基础上还需上调多少距离？（结果精确到 $0.1m)$（参考数据： $\sin 70°\approx 0.94$， $\cos 70°\approx 0.34$， $\tan 70°\approx 2.75$， $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

已知，点 $M$为二次函数 $y=-{(x-b)}^2+4b+1$图象的顶点，直线 $y=\mathit{mx}+5$分别交 $x$轴正半轴， $y$轴于点 $A$， $B$．

（1）判断顶点 $M$是否在直线 $y=4x+1$上，并说明理由．

（2）如图1，若二次函数图象也经过点 $A$， $B$，且 $\mathit{mx}+5>-{(x-b)}^2+4b+1$，根据图象，写出 $x$的取值范围．

（3）如图2，点 $A$坐标为 $(5,0)$，点 $M$在 $\mathit{\Delta AOB}$内，若点 $C(\frac{1}{4}$， $y_1)$， $D(\frac{3}{4}$， $y_2)$都在二次函数图象上，试比较 $y_1$与 $y_2$的大小．

我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”．

（1）概念理解：

如图1，在 $\mathit{\Delta ABC}$中， $\mathit{AC}=6$， $\mathit{BC}=3$， $\angle \mathit{ACB}=30°$，试判断 $\mathit{\Delta ABC}$是否是”等高底”三角形，请说明理由．

（2）问题探究：

如图2， $\mathit{\Delta ABC}$是“等高底”三角形， $\mathit{BC}$是”等底”，作 $\mathit{\Delta ABC}$关于 $\mathit{BC}$所在直线的对称图形得到△ $A^{\text{'}}\mathit{BC}$，连接 $\mathit{AA}\text{'}$交直线 $\mathit{BC}$于点 $D$．若点 $B$是△ $\mathit{AA}\text{'}C$的重心，求 $\frac{\mathit{AC}}{\mathit{BC}}$的值．

（3）应用拓展：

如图3，已知 $l_1//l_2$， $l_1$与 $l_2$之间的距离为2．“等高底” $\mathit{\Delta ABC}$的“等底” $\mathit{BC}$在直线 $l_1$上，点 $A$在直线 $l_2$上，有一边的长是 $\mathit{BC}$的 $\sqrt{2}$倍．将 $\mathit{\Delta ABC}$绕点 $C$按顺时针方向旋转 $45°$得到△ $A^{\text{'}}{B}^{\text{'}}C$， $A\text{'}C$所在直线交 $l_2$于点 $D$．求 $\mathit{CD}$的值．

已知， $\mathit{\Delta ABC}$中， $\angle B=\angle C$， $P$是 $\mathit{BC}$边上一点，作 $\angle \mathit{CPE}=\angle \mathit{BPF}$，分别交边 $\mathit{AC}$， $\mathit{AB}$于点 $E$， $F$．

（1）若 $\angle \mathit{CPE}=\angle C$（如图 $1)$，求证： $\mathit{PE}+\mathit{PF}=\mathit{AB}$．

（2）若 $\angle \mathit{CPE}\ne \angle C$，过点 $B$作 $\angle \mathit{CBD}=\angle \mathit{CPE}$，交 $\mathit{CA}$（或 $\mathit{CA}$的延长线）于点 $D$．试猜想：线段 $\mathit{PE}$， $\mathit{PF}$和 $\mathit{BD}$之间的数量关系，并就 $\angle \mathit{CPE}>\angle C$情形（如图 $2)$说明理由．

（3）若点 $F$与 $A$重合（如图 $3)$， $\angle C=27°$，且 $\mathit{PA}=\mathit{AE}$．

①求 $\angle \mathit{CPE}$的度数；

②设 $\mathit{PB}=a$， $\mathit{PA}=b$， $\mathit{AB}=c$，试证明： $b=\frac{a^2-c^2}{c}$．