2017年浙江省温州市中考数学试卷
某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有

A.75人B.100人C.125人D.200人
温州某企业车间有50名工人,某一天他们生产的机器零件个数统计如下表:
零件个数(个 |
5 |
6 |
7 |
8 |
人数(人 |
3 |
15 |
22 |
10 |
表中表示零件个数的数据中,众数是
A.5个B.6个C.7个D.8个
如图,一辆小车沿倾斜角为 的斜坡向上行驶13米,已知 ,则小车上升的高度是

A.5米B.6米C.6.5米D.12米
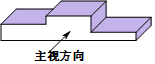
四个全等的直角三角形按图示方式围成正方形 ,过各较长直角边的中点作垂线,围成面积为 的小正方形 .已知 为 较长直角边, ,则正方形 的面积为

A. B. C. D.
我们把1,1,2,3,5,8,13,21, 这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作 圆弧 , , , 得到斐波那契螺旋线,然后顺次连接 , , , 得到螺旋折线(如图),已知点 , , ,则该折线上的点 的坐标为
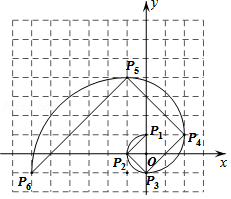
A. B. C. D.
甲、乙工程队分别承接了160米、200米的管道铺设任务,已知乙比甲每天多铺设5米,甲、乙完成铺设任务的时间相同,问甲每天铺设多少米?设甲每天铺设 米,根据题意可列出方程: .
如图, 矩形 的边 , 分别在 轴、 轴上, 点 在第一象限, 点 在边 上, 且 ,四边形 与四边形 关于直线 对称 (点 和 , 和 分别对应) . 若 ,反比例函数 的图象恰好经过点 , ,则 的值为 .
小明家的洗手盆上装有一种抬启式水龙头(如图 ,完全开启后,水流路线呈抛物线,把手端点 ,出水口 和落水点 恰好在同一直线上,点 至出水管 的距离为 ,洗手盆及水龙头的相关数据如图2所示,现用高 的圆柱型水杯去接水,若水流所在抛物线经过点 和杯子上底面中心 ,则点 到洗手盆内侧的距离 为 .

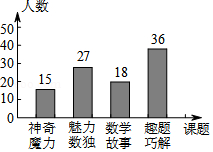
为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图.根据该统计图,请估计该校七年级480名学生选“数学故事”的人数.
(2)学校将选“数学故事”的学生分成人数相等的 , , 三个班,小聪、小慧都选择了“数学故事”,已知小聪不在 班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)
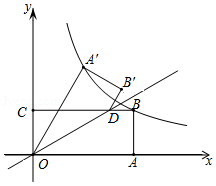
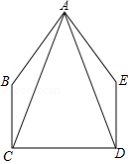
在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点 , ,请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个 ,使点 的横、纵坐标之和等于点 的横坐标;
(2)在图2中画一个 ,使点 , 横坐标的平方和等于它们纵坐标和的4倍.

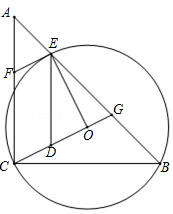
如图,在 中, , , (圆心 在 内部)经过 、 两点,交 于点 ,过点 作 的切线交 于点 .延长 交 于点 ,作 交 于点
(1)求证:四边形 是平行四边形;
(2)若 , ,求 的值.
如图,过抛物线 上一点 作 轴的平行线,交抛物线于另一点 ,交 轴于点 ,已知点 的横坐标为 .
(1)求抛物线的对称轴和点 的坐标;
(2)在 上任取一点 ,连接 ,作点 关于直线 的对称点 ;
①连接 ,求 的最小值;
②当点 落在抛物线的对称轴上,且在 轴上方时,求直线 的函数表达式.

小黄准备给长 ,宽 的长方形客厅铺设瓷砖,现将其划分成一个长方形 区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足 ,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元 ,面积为 ,区域Ⅱ的瓷砖均价为200元 ,且两区域的瓷砖总价为不超过12000元,求 的最大值;
(2)若区域Ⅰ满足 ,区域Ⅱ四周宽度相等
①求 , 的长;
②若甲、丙两瓷砖单价之和为300元 ,乙、丙瓷砖单价之比为 ,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.

 B.
B.
 D.
D.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号