2018年黑龙江省牡丹江市中考数学试卷
一组数据4,2, ,3,9的平均数为4,则这组数据的众数和中位数分别是
A.3,2B.2,2C.2,3D.2,4
如图,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为

A.35B.45C.55D.65
如图, 三个顶点的坐标分别是 , , ,将 绕着原点 旋转 ,得到△ ,则点 的坐标为

A. , 或 , B. , 或 ,
C. , 或 , D. , 或 ,
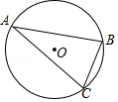
如图, 为矩形 的边 上一点,将矩形沿 折叠,使点 恰好落在 上的点 处,若 , ,则 的长为

A.6B.5C.4D.3
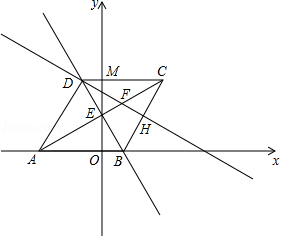
如图,正方形 中, 为 的中点, 的垂直平分线分别交 , 及 的延长线于点 , , ,连接 , , ,连接 并延长交 于点 .则下列结论中:
① ;② ;③ ;④ ;⑤
正确结论的个数有

A.2B.3C.4D.5
从党的“十八大”到“十九大”经历43800小时,我国的“天宫、蛟龙、天眼、悟空、墨子、大飞机”等各项科技创新成果“井喷”式发展,这些记录下了党的极不平凡的壮阔进程,请将数43800用科学记数法表示为
矩形 中, , ,点 在对角线 上,且 ,过点 作 交 于点 ,交 于点 .在 上取一点 ,使 ,则 的长为 .
如图,抛物线 经过 , 两点,交 轴于点 ,点 为抛物线的顶点,连接 ,点 为 的中点.请解答下列问题:
(1)求抛物线的解析式及顶点 的坐标;
(2)在 轴上找一点 ,使 的值最小,则 的最小值为 .
(注:抛物线 的对称轴是直线 ,顶点坐标为 ,
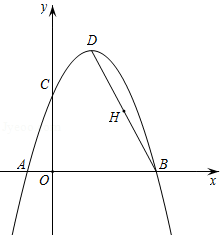
在四边形 中, , , , .以 为腰作等腰 ,使 ,过点 作 交直线 于点 .请画出图形,并直接写出 的长.
某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为 ,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?

在一条笔直的公路上依次有 , , 三地,甲、乙两人同时出发,甲从 地骑自行车去 地,途经 地休息1分钟,继续按原速骑行至 地,甲到达 地后,立即按原路原速返回 地;乙步行从 地前往 地.甲、乙两人距 地的路程 (米 与时间 (分 之间的函数关系如图所示,请结合图象解答下列问题:
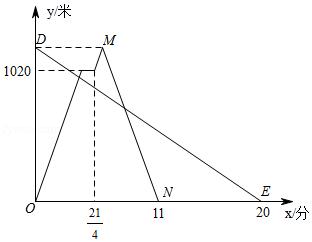
(1)请写出甲的骑行速度为 米 分,点 的坐标为 ;
(2)求甲返回时距 地的路程 与时间 之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回 地之前,经过多长时间两人距 地的路程相等.
在等腰 中, , 是 的角平分线,过点 作 于点 , .将 绕点 旋转,使 的两边交直线 于点 ,交直线 于点 ,请解答下列问题:
(1)当 绕点 旋转到如图①的位置时,求证: ;
(2)当 绕点 旋转到如图②,图③的位置时,请分别写出线段 , , 之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下, , ,则 , .

某书店现有资金7700元,计划全部用于购进甲、乙、丙三种图书共20套,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元.书店将甲、乙、丙三种图书的售价分别定为每套550元,430元,310元.设书店购进甲种图书 套,乙种图书 套,请解答下列问题:
(1)请求出 与 的函数关系式(不需要写出自变量的取值范围);
(2)若书店购进甲、乙两种图书均不少于1套,则该书店有几种进货方案?
(3)在(1)和(2)的条件下,根据市场调查,书店决定将三种图书的售价作如下调整:甲种图书的售价不变,乙种图书的售价上调 为正整数)元,丙种图书的售价下调 元,这样三种图书全部售出后,所获得的利润比(2)中某方案的利润多出20元,请直接写出书店是按哪种方案进的货及 的值.


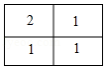 B.
B.
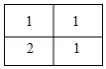 D.
D.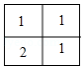


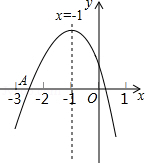

 粤公网安备 44130202000953号
粤公网安备 44130202000953号