2018年山东省青岛市中考数学试卷

观察下列四个图形，中心对称图形是 $($　　 $)$

A．B．C．D．

斑叶兰被列为国家二级保护植物，它的一粒种子重约0.0000005克．将0.0000005用科学记数法表示为 $($　　 $)$

A． $5\times {10}^7$B． $5\times {10}^{-7}$C． $0.5\times {10}^{-6}$D． $5\times {10}^{-6}$

如图，点 $A$所表示的数的绝对值是 $($　　 $)$

A．3B． $-3$C． $\frac{1}{3}$D． $-\frac{1}{3}$

计算 ${\left(a^2\right)}^3-5a^3·a^3$的结果是 $($　　 $)$

A． $a^5-5a^6$B． $a^6-5a^9$C． $-4a^6$D． $4a^6$

如图，点 $A$、 $B$、 $C$、 $D$在 $\odot O$上， $\angle \mathit{AOC}=140°$，点 $B$是 $\stackrel{̂}{\mathit{AC}}$的中点，则 $\angle D$的度数是 $($　　 $)$

A． $70°$B． $55°$C． $35.5°$D． $35°$

如图，三角形纸片 $\mathit{ABC}$， $\mathit{AB}=\mathit{AC}$， $\angle \mathit{BAC}=90°$，点 $E$为 $\mathit{AB}$中点．沿过点 $E$的直线折叠，使点 $B$与点 $A$重合，折痕 $\mathit{EF}$交 $\mathit{BC}$于点 $F$．已知 $\mathit{EF}=\frac{3}{2}$，则 $\mathit{BC}$的长是 $($　　 $)$

A． $\frac{3\sqrt{2}}{2}$B． $3\sqrt{2}$C．3D． $3\sqrt{3}$

如图，将线段 $\mathit{AB}$绕点 $P$按顺时针方向旋转 $90°$，得到线段 $A^{\text{'}}{B}^{\text{'}}$，其中点 $A$、 $B$的对应点分别是点 $A^{\text{'}}$、 $B^{\text{'}}$，则点 $A^{\text{'}}$的坐标是 $($　　 $)$

A． $(-1,3)$B． $(4,0)$C． $(3,-3)$D． $(5,-1)$

已知一次函数 $y=\frac{b}{a}x+c$的图象如图，则二次函数 $y=a{x}^2+\mathit{bx}+c$在平面直角坐标系中的图象可能是 $($　　 $)$

A．B．

C．D．

已知甲、乙两组数据的折线图如图，设甲、乙两组数据的方差分别为 $S_{甲}^2$、 $S_{乙}^2$，则 $S_{甲}^2$　　 $S_{乙}^2$（填“ $>$”、“ $=$”、“ $<$” $)$

计算： $2^{-1}\times \sqrt{12}+2\cos 30°=$　　．

5月份，甲、乙两个工厂用水量共为200吨．进入夏季用水高峰期后，两工厂积极响应国家号召，采取节水措施 $.6$月份，甲工厂用水量比5月份减少了 $15\%$，乙工厂用水量比5月份减少了 $10\%$，两个工厂6月份用水量共为174吨，求两个工厂5月份的用水量各是多少．设甲工厂5月份用水量为 $x$吨，乙工厂5月份用水量为 $y$吨，根据题意列关于 $x$， $y$的方程组为　　．

如图，已知正方形 $\mathit{ABCD}$的边长为5，点 $E$、 $F$分别在 $\mathit{AD}$、 $\mathit{DC}$上， $\mathit{AE}=\mathit{DF}=2$， $\mathit{BE}$与 $\mathit{AF}$相交于点 $G$，点 $H$为 $\mathit{BF}$的中点，连接 $\mathit{GH}$，则 $\mathit{GH}$的长为　　．

如图， $\text{Rt}\Delta \text{ABC}$， $\angle B=90°$， $\angle C=30°$， $O$为 $\mathit{AC}$上一点， $\mathit{OA}=2$，以 $O$为圆心，以

$\mathit{OA}$为半径的圆与 $\mathit{CB}$相切于点 $E$，与 $\mathit{AB}$相交于点 $F$，连接 $\mathit{OE}$、 $\mathit{OF}$，则图中阴影部分的面积是　　．

一个由16个完全相同的小立方块搭成的几何体，其最下面一层摆放了9个小立方块，它的主视图和左视图如图所示，那么这个几何体的搭法共有　 种．

已知：如图， $\angle \mathit{ABC}$，射线 $\mathit{BC}$上一点 $D$．

求作：等腰 $\mathit{\Delta PBD}$，使线段 $\mathit{BD}$为等腰 $\mathit{\Delta PBD}$的底边，点 $P$在 $\angle \mathit{ABC}$内部，且点 $P$到 $\angle \mathit{ABC}$两边的距离相等．

（1）解不等式组： $\left\{\begin{array}{c}\frac{x-2}{3}<1\\ 2x+16>14\end{array}\right.$

（2）化简： $(\frac{x^2+1}{x}-2)·\frac{x}{x^2-1}$．

小明和小亮计划暑期结伴参加志愿者活动．小明想参加敬老服务活动，小亮想参加文明礼仪宣传活动．他们想通过做游戏来决定参加哪个活动，于是小明设计了一个游戏，游戏规则是：在三张完全相同的卡片上分别标记4、5、6三个数字，一人先从三张卡片中随机抽出一张，记下数字后放回，另一人再从中随机抽出一张，记下数字，若抽出的两张卡片标记的数字之和为偶数，则按照小明的想法参加敬老服务活动，若抽出的两张卡片标记的数字之和为奇数，则按照小亮的想法参加文明礼仪宣传活动．你认为这个游戏公平吗？请说明理由．

八年级（1）班研究性学习小组为研究全校同学课外阅读情况，在全校随机邀请了部分同学参与问卷调查，统计同学们一个月阅读课外书的数量，并绘制了以下统计图．

请根据图中信息解决下列问题：

（1）共有　　名同学参与问卷调查；

（2）补全条形统计图和扇形统计图；

（3）全校共有学生1500人，请估计该校学生一个月阅读2本课外书的人数约为多少．

某区域平面示意图如图，点 $O$在河的一侧， $\mathit{AC}$和 $\mathit{BC}$表示两条互相垂直的公路．甲勘测员在 $A$处测得点 $O$位于北偏东 $45°$，乙勘测员在 $B$处测得点 $O$位于南偏西 $73.7°$，测得 $\mathit{AC}=840m$， $\mathit{BC}=500m$．请求出点 $O$到 $\mathit{BC}$的距离．

参考数据： $\sin 73.7°\approx \frac{24}{25}$， $\cos 73.7°\approx \frac{7}{25}$， $\tan 73.7°\approx \frac{24}{7}$

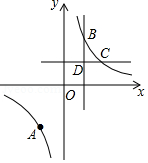
已知反比例函数的图象经过三个点 $A(-4,-3)$， $B(2m,y_1)$， $C(6m,y_2)$，其中 $m>0$．

（1）当 $y_1-y_2=4$时，求 $m$的值；

（2）如图，过点 $B$、 $C$分别作 $x$轴、 $y$轴的垂线，两垂线相交于点 $D$，点 $P$在 $x$轴上，若三角形 $\mathit{PBD}$的面积是8，请写出点 $P$坐标（不需要写解答过程）．

已知：如图，平行四边形 $\mathit{ABCD}$，对角线 $\mathit{AC}$与 $\mathit{BD}$相交于点 $E$，点 $G$为 $\mathit{AD}$的中点，连接 $\mathit{CG}$， $\mathit{CG}$的延长线交 $\mathit{BA}$的延长线于点 $F$，连接 $\mathit{FD}$．

（1）求证： $\mathit{AB}=\mathit{AF}$；

（2）若 $\mathit{AG}=\mathit{AB}$， $\angle \mathit{BCD}=120°$，判断四边形 $\mathit{ACDF}$的形状，并证明你的结论．

某公司投入研发费用80万元 $(80$万元只计入第一年成本），成功研发出一种产品．公司按订单生产（产量 $=$销售量），第一年该产品正式投产后，生产成本为6元 $/$件．此产品年销售量 $y$（万件）与售价 $x$（元 $/$件）之间满足函数关系式 $y=-x+26$．

（1）求这种产品第一年的利润 $W_1$（万元）与售价 $x$（元 $/$件）满足的函数关系式；

（2）若该产品第一年的利润为20万元，那么该产品第一年的售价是多少？

（3）在（2）的条件下，第二年，该公司将第一年的利润20万元 $(20$万元只计入第二年成本）再次投入研发，使产品的生产成本降为5元 $/$件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．请计算该公司第二年的利润 $W_2$至少为多少万元．

问题提出：用若干相同的一个单位长度的细直木棒，按照如图1方式搭建一个长方体框架，探究所用木棒条数的规律．

问题探究：

我们先从简单的问题开始探究，从中找出解决问题的方法．

探究一

用若干木棒来搭建横长是 $m$，纵长是 $n$的矩形框架 $(m$、 $n$是正整数），需要木棒的条数．

如图①，当 $m=1$， $n=1$时，横放木棒为 $1\times (1+1)$条，纵放木棒为 $(1+1)\times 1$条，共需4条；

如图②，当 $m=2$， $n=1$时，横放木棒为 $2\times (1+1)$条，纵放木棒为 $(2+1)\times 1$条，共需7条；

如图③，当 $m=2$， $n=2$时，横放木棒为 $2\times (2+1)$条，纵放木棒为 $(2+1)\times 2$条，共需12条；

如图④，当 $m=3$， $n=1$时，横放木棒为 $3\times (1+1)$条，纵放木棒为 $(3+1)\times 1$条，共需10条；

如图⑤，当 $m=3$， $n=2$时，横放木棒为 $3\times (2+1)$条，纵放木棒为 $(3+1)\times 2$条，共需17条．

问题（一 $)$：当 $m=4$， $n=2$时，共需木棒　　条．

问题（二 $)$：当矩形框架横长是 $m$，纵长是 $n$时，横放的木棒为　　条，

纵放的木棒为　　条．

探究二

用若干木棒来搭建横长是 $m$，纵长是 $n$，高是 $s$的长方体框架 $(m$、 $n$、 $s$是正整数），需要木棒的条数．

如图⑥，当 $m=3$， $n=2$， $s=1$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (1+1)=34$条，竖放木棒为 $(3+1)\times (2+1)\times 1=12$条，共需46条；

如图⑦，当 $m=3$， $n=2$， $s=2$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (2+1)=51$条，竖放木棒为 $(3+1)\times (2+1)\times 2=24$条，共需75条；

如图⑧，当 $m=3$， $n=2$， $s=3$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (3+1)=68$条，竖放木棒为 $(3+1)\times (2+1)\times 3=36$条，共需104条．

问题（三 $)$：当长方体框架的横长是 $m$，纵长是 $n$，高是 $s$时，横放与纵放木棒条数之和为　　条，竖放木棒条数为　　条．

实际应用：现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架，总共使用了170条木棒，则这个长方体框架的横长是　　．

拓展应用：若按照如图2方式搭建一个底面边长是10，高是5的正三棱柱框架，需要木棒　　条．

已知：如图，四边形 $\mathit{ABCD}$， $\mathit{AB}//\mathit{DC}$， $\mathit{CB}\perp \mathit{AB}$， $\mathit{AB}=16\mathit{cm}$， $\mathit{BC}=6\mathit{cm}$， $\mathit{CD}=8\mathit{cm}$，动点 $P$从点 $D$开始沿 $\mathit{DA}$边匀速运动，动点 $Q$从点 $A$开始沿 $\mathit{AB}$边匀速运动，它们的运动速度均为 $2\mathit{cm}/s$．点 $P$和点 $Q$同时出发，以 $\mathit{QA}$、 $\mathit{QP}$为边作平行四边形 $\mathit{AQPE}$，设运动的时间为 $t\left(s\right)$， $0<t<5$．

根据题意解答下列问题：

（1）用含 $t$的代数式表示 $\mathit{AP}$；

（2）设四边形 $\mathit{CPQB}$的面积为 $S\left(c{m}^2\right)$，求 $S$与 $t$的函数关系式；

（3）当 $\mathit{QP}\perp \mathit{BD}$时，求 $t$的值；

（4）在运动过程中，是否存在某一时刻 $t$，使点 $E$在 $\angle \mathit{ABD}$的平分线上？若存在，求出 $t$的值；若不存在，请说明理由．