2016年广西贵港市中考数学试卷
在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1)B.(﹣1,﹣2)C.(﹣1,2)D.(1,2)
下列命题中错误的是( )
A.两组对角分别相等的四边形是平行四边形
B.矩形的对角线相等
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分且相等的四边形是正方形
若关于x的一元二次方程x2﹣3x+p=0(p≠0)的两个不相等的实数根分别为a和b,且a2﹣ab+b2=18,则 的值是( )
A.3B.﹣3C.5D.﹣5
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°, ,则这个圆锥底面圆的半径是( )

A. B. C. D.
如图,抛物线 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )

A.(4,3)B.(5, )C.(4, )D.(5,3)
如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S▱ABCD=AC•BC;③OE:AC= :6;④S△OCF=2S△OEF
:6;④S△OCF=2S△OEF
成立的个数有( )

A.1个B.2个C.3个D.4个
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (结果保留π).

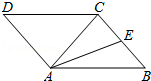
如图,在▱ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
如图,已知一次函数 的图象与反比例函数 的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 x+b<
x+b< 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.

在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:

(1)本次接受问卷调查的学生总人数是 ;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为 ,m的值为 ;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.
为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.
(1)求2014至2016年该市投入科研经费的年平均增长率;
(2)根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a万元,请求出a的取值范围.
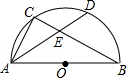
如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC= ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.

如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号