2020年湖北省随州市中考数学试卷
随州7月份连续5天的最高气温分别为:29,30,32,30,34(单位: ,则这组数据的众数和中位数分别为
| A. |
30,32 |
B. |
31,30 |
C. |
30,31 |
D. |
30,30 |
我国古代数学著作《孙子算经》中有"鸡兔同笼"问题:"今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何".设鸡有 只,兔有 只,则根据题意,下列方程组中正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
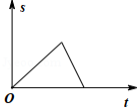
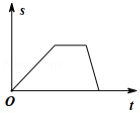
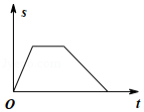
小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离 与出发时间 之间的对应关系的是
| A. |
|
B. |
|
| C. |
|
D. |
|
设边长为 的等边三角形的高、内切圆的半径、外接圆的半径分别为 、 、 ,则下列结论不正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
将关于 的一元二次方程 变形为 ,就可以将 表示为关于 的一次多项式,从而达到"降次"的目的,又如 ,我们将这种方法称为"降次法",通过这种方法可以化简次数较高的代数式.根据"降次法",已知: ,且 ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
|
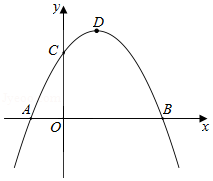
如图所示,已知二次函数 的图象与 轴交于 , 两点,与 轴的正半轴交于点 ,顶点为 ,则下列结论:
① ;
② ;
③当 是等腰三角形时, 的值有2个;
④当 是直角三角形时, .
其中正确的有
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
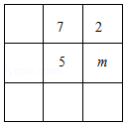
幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方九宫图.将数字分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则的值为 .
如图,已知矩形中,,,点,分别在边,上,沿着折叠矩形,使点,分别落在,处,且点在线段上(不与两端点重合),过点作于点,连接,给出下列判断:
①;
②折痕的长度的取值范围为;
③当四边形为正方形时,为的中点;
④若,则折叠后重叠部分的面积为.
其中正确的是 .(写出所有正确判断的序号)

已知关于 的一元二次方程 .
(1)求证:无论 取何值,此方程总有两个不相等的实数根;
(2)若方程有两个实数根 , ,且 ,求 的值.
根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展"一带一盔"安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:
年龄 (岁 |
人数 |
男性占比 |
|
4 |
|
|
|
|
|
25 |
|
|
8 |
|
|
3 |
|
(1)统计表中 的值为 ;
(2)若要按照表格中各年龄段的人数来绘制扇形统计图,则年龄在" "部分所对应扇形的圆心角的度数为 ;
(3)在这50人中女性有 人;
(4)若从年龄在" "的4人中随机抽取2人参加交通安全知识学习,请用列表或画树状图的方法,求恰好抽到2名男性的概率.
如图,某楼房 顶部有一根天线 ,为了测量天线的高度,在地面上取同一条直线上的三点 , , ,在点 处测得天线顶端 的仰角为 ,从点 走到点 ,测得 米,从点 测得天线底端 的仰角为 ,已知 , , 在同一条垂直于地面的直线上, 米.
(1)求 与 之间的距离;
(2)求天线 的高度.(参考数据: ,结果保留整数)

如图,在 中, ,以斜边 上的中线 为直径作 ,与 交于点 ,与 的另一个交点为 ,过 作 ,垂足为 .
(1)求证: 是 的切线;
(2)若 的直径为5, ,求 的长.

2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格 (元 只)和销量 (只 与第 天的关系如下表:
第 天 |
1 |
2 |
3 |
4 |
5 |
销售价格 (元 只) |
2 |
3 |
4 |
5 |
6 |
销量 (只 |
70 |
75 |
80 |
85 |
90 |
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元 只,该药店从第6天起将该型号口罩的价格调整为1元 只.据统计,该药店从第6天起销量 (只 与第 天的关系为 ,且 为整数),已知该型号口罩的进货价格为0.5元 只.
(1)直接写出该药店该月前5天的销售价格 与 和销量 与 之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润 (元 与 的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以 倍的罚款,若罚款金额不低于2000元,则 的取值范围为 .
勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有"若勾三,股四,则弦五"的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅"弦图"(如图 ,后人称之为"赵爽弦图",流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)

(2)①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足 的有 个;

②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 , ,直角三角形面积为 ,请判断 , , 的关系并证明;
(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的"勾股树".在如图9所示的"勾股树"的某部分图形中,设大正方形 的边长为定值 ,四个小正方形 , , , 的边长分别为 , , , ,已知 ,则当 变化时,回答下列问题:(结果可用含 的式子表示)
① ;
② 与 的关系为 , 与 的关系为 .

如图,在平面直角坐标系中,抛物线 的对称轴为直线 ,其图象与 轴交于点 和点 ,与 轴交于点 .

(1)直接写出抛物线的解析式和 的度数;
(2)动点 , 同时从 点出发,点 以每秒3个单位的速度在线段 上运动,点 以每秒 个单位的速度在线段 上运动,当其中一个点到达终点时,另一个点也随之停止运动.设运动的时间为 秒,连接 ,再将线段 绕点 顺时针旋转 ,设点 落在点 的位置,若点 恰好落在抛物线上,求 的值及此时点 的坐标;
(3)在(2)的条件下,设 为抛物线上一动点, 为 轴上一动点,当以点 , , 为顶点的三角形与 相似时,请直接写出点 及其对应的点 的坐标.(每写出一组正确的结果得1分,至多得4分)






 粤公网安备 44130202000953号
粤公网安备 44130202000953号