2019年浙江省台州市中考数学试卷
2019年台州市计划安排重点建设项目344个,总投资595200000000元.用科学记数法可将595200000000表示为
| A. |
|
B. |
|
C. |
|
D. |
|
方差是刻画数据波动程度的量.对于一组数据 , , , , ,可用如下算式计算方差: ,其中"5"是这组数据的
| A. |
最小值 |
B. |
平均数 |
C. |
中位数 |
D. |
众数 |
一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走 ,平路每小时走 ,下坡每小时走 ,那么从甲地到乙地需 ,从乙地到甲地需 .甲地到乙地全程是多少? |
小红将这个实际问题转化为二元一次方程组问题,设未知数 , ,已经列出一个方程 ,则另一个方程正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,等边三角形 的边长为8,以 上一点 为圆心的圆分别与边 , 相切,则 的半径为

| A. |
|
B. |
3 |
C. |
4 |
D. |
|
如图,有两张矩形纸片 和 , , .把纸片 交叉叠放在纸片 上,使重叠部分为平行四边形,且点 与点 重合.当两张纸片交叉所成的角 最小时, 等于

| A. |
|
B. |
|
C. |
|
D. |
|
已知某函数的图象 与函数 的图象关于直线 对称.下列命题:①图象 与函数 的图象交于点 , ;②点 , 在图象 上;③图象 上的点的纵坐标都小于4;④ , , , 是图象 上任意两点,若 ,则 .其中真命题是
| A. |
①② |
B. |
①③④ |
C. |
②③④ |
D. |
①②③④ |
如图是用8块 型瓷砖(白色四边形)和8块 型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中 型瓷砖的总面积与 型瓷砖的总面积之比为

| A. |
|
B. |
|
C. |
|
D. |
|
一个不透明的布袋中仅有2个红球,1个黑球,这些球除颜色外无其它差别.先随机摸出一个小球,记下颜色后放回搅匀,再随机摸出一个小球,则两次摸出的小球颜色不同的概率是 .
砸“金蛋”游戏:把210个“金蛋”连续编号为1,2,3,,210,接着把编号是3的整数倍的“金蛋”全部砸碎;然后将剩下的“金蛋”重新连续编号为1,2,3,,接着把编号是3的整数倍的“金蛋”全部砸碎按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止.操作过程中砸碎编号是“66”的“金蛋”共 个.
如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为 .
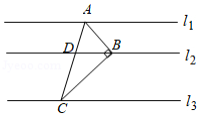
图1是一辆在平地上滑行的滑板车,图2是其示意图.已知车杆长,车杆与脚踏板所成的角,前后轮子的半径均为,求把手离地面的高度(结果保留小数点后一位;参考数据:,,.

如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度(单位:与下行时间(单位:之间具有函数关系,乙离一楼地面的高度(单位:与下行时间(单位:的函数关系如图2所示.
(1)求关于的函数解析式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.

安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.

(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于,可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.
(1)已知凸五边形的各条边都相等.
①如图1,若,求证:五边形是正五边形;
②如图2,若,请判断五边形是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”
如图3,已知凸六边形的各条边都相等.
①若,则六边形是正六边形;
②若,则六边形是正六边形.

已知函数,为常数)的图象经过点.
(1)求,满足的关系式;
(2)设该函数图象的顶点坐标是,当的值变化时,求关于的函数解析式;
(3)若该函数的图象不经过第三象限,当时,函数的最大值与最小值之差为16,求的值.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号