2018年重庆市中考数学试卷(b卷)
下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片, ,按此规律排列下去第⑥个图中黑色正方形纸片的张数为

| A. |
11 |
B. |
13 |
C. |
15 |
D. |
17 |
下列调查中,最适合采用全面调查(普查)的是
| A. |
对我市中学生每周课外阅读时间情况的调查 |
| B. |
对我市市民知晓"礼让行人"交通新规情况的调查 |
| C. |
对我市中学生观看电影《厉害了,我的国》情况的调查 |
| D. |
对我国首艘国产航母002型各零部件质量情况的调查 |
制作一块 长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是
| A. |
360元 |
B. |
720元 |
C. |
1080元 |
D. |
2160元 |
下列命题是真命题的是
| A. |
如果一个数的相反数等于这个数本身,那么这个数一定是0 |
| B. |
如果一个数的倒数等于这个数本身,那么这个数一定是1 |
| C. |
如果一个数的平方等于这个数本身,那么这个数一定是0 |
| D. |
如果一个数的算术平方根等于这个数本身,那么这个数一定是0 |
根据如图所示的程序计算函数 的值,若输入的 值是4或7时,输出的 值相等,则 等于

| A. |
9 |
B. |
7 |
C. |
|
D. |
|
如图, 是一垂直于水平面的建筑物,某同学从建筑物底端 出发,先沿水平方向向右行走20米到达点 ,再经过一段坡度(或坡比)为 、坡长为10米的斜坡 到达点 ,然后再沿水平方向向右行走40米到达点 , , , , 均在同一平面内).在 处测得建筑物顶端 的仰角为 ,则建筑物 的高度约为(参考数据: , ,

| A. |
21.7米 |
B. |
22.4米 |
C. |
27.4米 |
D. |
28.8米 |
如图, 中, ,点 是边 上一点,以点 为圆心,以 为半径作圆, 恰好与 相切于点 ,连接 .若 平分 , ,则线段 的长是
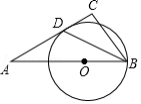
| A. |
2 |
B. |
|
C. |
|
D. |
|
如图,菱形 的边 轴,垂足为点 ,顶点 在第二象限,顶点 在 轴的正半轴上,反比例函数 的图象同时经过顶点 , .若点 的横坐标为5, ,则 的值为

| A. |
|
B. |
3 |
C. |
|
D. |
5 |
若数 使关于 的不等式组 ,有且仅有三个整数解,且使关于 的分式方程 有整数解,则满足条件的所有 的值之和是
| A. |
|
B. |
|
C. |
|
D. |
|
某企业对一工人在五个工作日里生产零件的数量进行调查,并绘制了如图所示的折线统计图,则在这五天里该工人每天生产零件的平均数是 个.

一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离(米与小玲从家出发后步行的时间(分之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为 米.

为实现营养套餐的合理搭配,某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮.甲种袋装粗粮每袋含有3千克粗粮,1千克粗粮,1千克粗粮;乙种袋装粗粮每袋含有1千克粗粮,2千克粗粮,2千克粗粮.甲、乙两种袋装粗粮每袋成本分别等于袋中的、、三种粗粮成本之和.已知每袋甲种粗粮的成本是每千克种粗粮成本的7.5倍,每袋乙种粗粮售价比每袋甲种粗粮售价高,乙种袋装粗粮的销售利润率是.当销售这两款袋装粗粮的销售利润率为时,该电商销售甲、乙两种袋装粗粮的袋数之比是 (商品的销售利润率
某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:.模拟驾驶;.军事竞技;.家乡导游;.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)八年级(3)班学生总人数是 ,并将条形统计图补充完整;
(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这些学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.

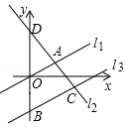
如图,在平面直角坐标系中,直线与直线交点的横坐标为2,将直线沿轴向下平移4个单位长度,得到直线,直线与轴交于点,与直线交于点,点的纵坐标为.直线与轴交于点.
(1)求直线的解析式;
(2)求的面积.
在美丽乡村建设中,某县政府投入专项资金,用于乡村沼气池和垃圾集中处理点建设.该县政府计划:2018年前5个月,新建沼气池和垃圾集中处理点共计50个,且沼气池的个数不低于垃圾集中处理点个数的4倍.
(1)按计划,2018年前5个月至少要修建多少个沼气池?
(2)到2018年5月底,该县按原计划刚好完成了任务,共花费资金78万元,且修建的沼气池个数恰好是原计划的最小值.据核算,前5个月,修建每个沼气池与垃圾集中处理点的平均费用之比为.为加大美丽乡村建设的力度,政府计划加大投入,今年后7个月,在前5个月花费资金的基础上增加投入,全部用于沼气池和垃圾集中处理点建设.经测算:从今年6月起,修建每个沼气池与垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加,,新建沼气池与垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加,,求的值.
如图,在中,,点在对角线上,,于点,的延长线交于点.点在的延长线上,且,连接.
(1)若,,求的长;
(2)求证:.

对任意一个四位数,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称为“极数”.
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数是另一个正整数的平方,则称正整数是完全平方数.若四位数为“极数”,记,求满足是完全平方数的所有.
抛物线与轴交于点,(点在点的左边),与轴交于点,点是该抛物线的顶点.
(1)如图1,连接,求线段的长;
(2)如图2,点是直线上方抛物线上一点,轴于点,与线段交于点;将线段沿轴左右平移,线段的对应线段是,当的值最大时,求四边形周长的最小值,并求出对应的点的坐标;
(3)如图3,点是线段的中点,连接,将沿直线翻折至△的位置,再将△绕点旋转一周,在旋转过程中,点,的对应点分别是点,,直线分别与直线,轴交于点,.那么,在△的整个旋转过程中,是否存在恰当的位置,使是以为腰的等腰三角形?若存在,请直接写出所有符合条件的线段的长;若不存在,请说明理由.








 粤公网安备 44130202000953号
粤公网安备 44130202000953号