2016年江西省中考数学试卷
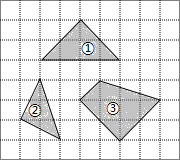
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③ 的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为 ,水平部分线段长度之和记为 ,则这三个多边形中满足 的是
| A. |
只有② |
B. |
只有③ |
C. |
②③ |
D. |
①②③ |
如图是一张长方形纸片 ,已知 , , 为 上一点, ,现要剪下一张等腰三角形纸片 ,使点 落在长方形 的某一条边上,则等腰三角形 的底边长是 .

如图,过点 的两条直线 , 分别交 轴于点 , ,其中点 在原点上方,点 在原点下方,已知 .
(1)求点 的坐标;
(2)若 的面积为4,求直线 的解析式.

为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的"您最关心孩子哪方面成长"的主题调查,调查设置了"健康安全"、"日常学习"、"习惯养成"、"情感品质"四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子"情感品质"方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?

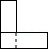
如图,六个完全相同的小长方形拼成了一个大长方形, 是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
(1)在图1中画出一个 角,使点 或点 是这个角的顶点,且 为这个角的一边;
(2)在图2中画出线段 的垂直平分线.

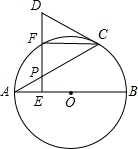
如图, 是 的直径,点 是弦 上一动点(不与 , 重合),过点 作 ,垂足为 ,射线 交 于点 ,交过点 的切线于点 .
(1)求证: ;
(2)若 ,当 是 的中点时,判断以 , , , 为顶点的四边形是什么特殊四边形?说明理由.
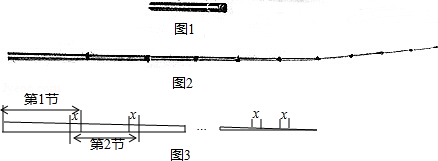
如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长 ,第2节套管长 ,以此类推,每一节套管均比前一节套管少 .完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为 .
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为 ,求 的值.
甲、乙两人利用扑克牌玩"10点"游戏,游戏规则如下:
①将牌面数字作为"点数",如红桃6的"点数"就是6(牌面点数与牌的花色无关);
②两人摸牌结束时,将所摸牌的"点数"相加,若"点数"之和小于或等于10,此时"点数"之和就是"最终点数";若"点数"之和大于10,则"最终点数"是0;
③游戏结束前双方均不知道对方"点数";
④判定游戏结果的依据是:"最终点数"大的一方获胜,"最终点数"相等时不分胜负.
现甲、乙均各自摸了两张牌,数字之和都是5,这时桌上还有四张背面朝上的扑克牌,牌面数字分别是4,5,6,7.
(1)若甲从桌上继续摸一张扑克牌,乙不再摸牌,则甲获胜的概率为 ;
(2)若甲先从桌上继续摸一张扑克牌,接着乙从剩下的扑克牌中摸出一张牌,然后双方不再摸牌.请用树状图或表格表示出这次摸牌后所有可能的结果,再列表呈现甲、乙的"最终点数",并求乙获胜的概率.

如图1是一副创意卡通圆规,图2是其平面示意图, 是支撑臂, 是旋转臂,使用时,以点 为支撑点,铅笔芯端点 可绕点 旋转作出圆.已知 .
(1)当 时,求所作圆的半径;(结果精确到
(2)保持 不变,在旋转臂 末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到
(参考数据: , , , ,可使用科学计算器)

如图,将正 边形绕点 顺时针旋转 后,发现旋转前后两图形有另一交点 ,连接 ,我们称 为"叠弦";再将"叠弦" 所在的直线绕点 逆时针旋转 后,交旋转前的图形于点 ,连接 ,我们称 为"叠弦角", 为"叠弦三角形".
[探究证明]
(1)请在图1和图2中选择其中一个证明:"叠弦三角形" 是等边三角形;
(2)如图2,求证: .
[归纳猜想]
(3)图1、图2中的"叠弦角"的度数分别为 , ;
(4)图 中,"叠弦三角形" 等边三角形(填"是"或"不是"
(5)图 中,"叠弦角"的度数为 (用含 的式子表示)













 粤公网安备 44130202000953号
粤公网安备 44130202000953号