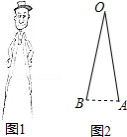
如图1是一副创意卡通圆规,图2是其平面示意图, 是支撑臂, 是旋转臂,使用时,以点 为支撑点,铅笔芯端点 可绕点 旋转作出圆.已知 .
(1)当 时,求所作圆的半径;(结果精确到
(2)保持 不变,在旋转臂 末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到
(参考数据: , , , ,可使用科学计算器)
相关知识点
推荐套卷
如图1是一副创意卡通圆规,图2是其平面示意图, 是支撑臂, 是旋转臂,使用时,以点 为支撑点,铅笔芯端点 可绕点 旋转作出圆.已知 .
(1)当 时,求所作圆的半径;(结果精确到
(2)保持 不变,在旋转臂 末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到
(参考数据: , , , ,可使用科学计算器)
