初中数学一次函数试题

探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程．以下是我们研究函数 $y=x+|-2x+6|+m$ 性质及其应用的部分过程，请按要求完成下列各小题．

$x$	$\dots$	$-2$	$-1$	0	1	2	3	4	5	$\dots$
$y$	$\dots$	6	5	4	$a$	2	1	$b$	7	$\dots$

（1）写出函数关系式中 $m$ 及表格中 $a$ ， $b$ 的值：

$m=$　　， $a=$　　， $b=$　　；

（2）根据表格中的数据在所给的平面直角坐标系中画出该函数的图象，并根据图象写出该函数的一条性质： 　　；

（3）已知函数 $y=\frac{16}{x}$ 的图象如图所示，结合你所画的函数图象，直接写出不等式 $x+|-2x+6|+m>\frac{16}{x}$ 的解集．

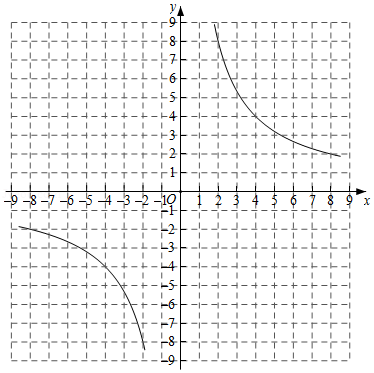
在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质及其应用的过程．以下是我们研究函数 $y=\frac{4-x^2}{x^2+1}$ 的性质及其应用的部分过程，请按要求完成下列各小题．

（1）请把下表补充完整，并在给出的图中补全该函数的大致图象；

$x$	$\dots$	$-5$	$-4$	$-3$	$-2$	$-1$	0	1	2	3	4	5	$\dots$
$y=\frac{4-x^2}{x^2+1}$	$\dots$	$-\frac{21}{26}$	$-\frac{12}{17}$	$-\frac{1}{2}$	0	$\frac{3}{2}$	4	$\frac{3}{2}$	0				$\dots$

（2）请根据这个函数的图象，写出该函数的 $\text{"}D$ 条性质；

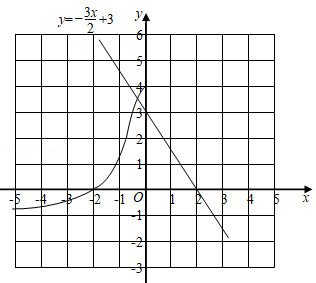
（3）已知函数 $y=-\frac{3}{2}x+3$ 的图象如图所示．根据函数图象，直接写出不等式 $-\frac{3}{2}x+3>\frac{4-x^2}{x^2+1}$ 的解集．（近似值保留一位小数，误差不超过 $0.2)$

甲无人机从地面起飞，乙无人机从距离地面 $20m$ 高的楼顶起飞，两架无人机同时匀速上升 $10s$ ．甲、乙两架无人机所在的位置距离地面的高度 $y$ （单位： $m)$ 与无人机上升的时间 $x$ （单位： $s)$ 之间的关系如图所示．下列说法正确的是 $($ 　　 $)$

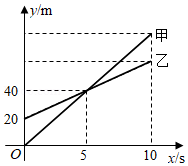
A．	$5s$ 时，两架无人机都上升了 $40m$
B．	$10s$ 时，两架无人机的高度差为 $20m$
C．	乙无人机上升的速度为 $8m/s$
D．	$10s$ 时，甲无人机距离地面的高度是 $60m$

某公司生产的一种营养品信息如表．已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克．

营养品信息表
营养成份	每千克含铁42毫克
配料表	原料	每千克含铁
	甲食材	50毫克
	乙食材	10毫克
规格	每包食材含量	每包单价
$A$ 包装	1千克	45元
$B$ 包装	0.25千克	12元

（1）问甲、乙两种食材每千克进价分别是多少元？

（2）该公司每日用18000元购进甲、乙两种食材并恰好全部用完．

①问每日购进甲、乙两种食材各多少千克？

②已知每日其他费用为2000元，且生产的营养品当日全部售出．若 $A$ 的数量不低于 $B$ 的数量，则 $A$ 为多少包时，每日所获总利润最大？最大总利润为多少元？

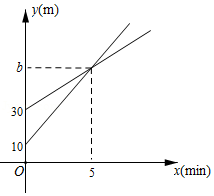
Ⅰ号无人机从海拔 $10m$ 处出发，以 $10m/\mathit{min}$ 的速度匀速上升，Ⅱ号无人机从海拔 $30m$ 处同时出发，以 $a(m/\mathit{min})$ 的速度匀速上升，经过 $5\mathit{min}$ 两架无人机位于同一海拔高度 $b\left(m\right)$ ．无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系如图．两架无人机都上升了 $15\mathit{min}$ ．

（1）求 $b$ 的值及Ⅱ号无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系式；

（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

某通讯公司就手机流量套餐推出三种方案，如下表：

	$A$ 方案	$B$ 方案	$C$ 方案
每月基本费用（元 $)$	20	56	266
每月免费使用流量（兆 $)$	1024	$m$	无限
超出后每兆收费（元 $)$	$n$	$n$

$A$ ， $B$ ， $C$ 三种方案每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系如图所示．

（1）请写出 $m$ ， $n$ 的值．

（2）在 $A$ 方案中，当每月使用的流量不少于1024兆时，求每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系式．

（3）在这三种方案中，当每月使用的流量超过多少兆时，选择 $C$ 方案最划算？

李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程 $s$ （千米）与行驶时间 $t$ （小时）的关系如图所示（中途休息、加油的时间不计）．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升 $/$ 千米，请根据图象解答下列问题：

（1）写出工厂离目的地的路程；

（2）求 $s$ 关于 $t$ 的函数表达式；

（3）当货车显示加油提醒后，问行驶时间 $t$ 在怎样的范围内货车应进站加油？

已知点 $P(a,b)$ 在直线 $y=-3x-4$ 上，且 $2a-5b⩽0$ ，则下列不等式一定成立的是 $($ 　　 $)$

A．

$\frac{a^{}}{b}⩽\frac{5^{}}{2}$

B．

$\frac{a^{}}{b}⩾\frac{5^{}}{2}$

C．

$\frac{b}{a}⩾\frac{2}{5}$

D．

$\frac{b}{a}⩽\frac{2}{5}$

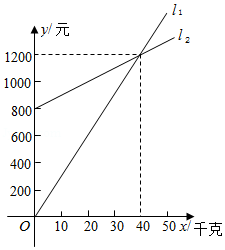
某鲜花销售公司每月付给销售人员的工资有两种方案．

方案一：没有底薪，只付销售提成；

方案二：底薪加销售提成．

如图中的射线 $l_1$ ，射线 $l_2$ 分别表示该鲜花销售公司每月按方案一，方案二付给销售人员的工资 $y_1$ （单位：元）和 $y_2$ （单位：元）与其当月鲜花销售量 $x$ （单位：千克） $(x⩾0)$ 的函数关系．

（1）分别求 $y_1$ 、 $y_2$ 与 $x$ 的函数解析式（解析式也称表达式）；

（2）若该公司某销售人员今年3月份的鲜花销售量没有超过70千克，但其3月份的工资超过2000元．这个公司采用了哪种方案给这名销售人员付3月份的工资？

在"看图说故事"活动中，某学习小组结合图象设计了一个问题情境．已知学校、书店、陈列馆依次在同一条直线上，书店离学校 $12\mathit{km}$ ，陈列馆离学校 $20\mathit{km}$ ．李华从学校出发，匀速骑行 $0.6h$ 到达书店；在书店停留 $0.4h$ 后，匀速骑行 $0.5h$ 到达陈列馆；在陈列馆参观学习一段时间，然后回学校；回学校途中，匀速骑行 $0.5h$ 后减速，继续匀速骑行回到学校．给出的图象反映了这个过程中李华离学校的距离 $y\mathit{km}$ 与离开学校的时间 $xh$ 之间的对应关系．

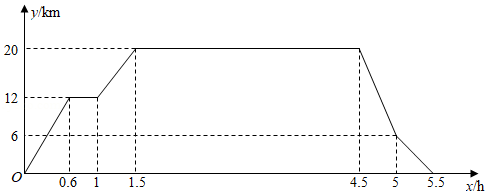
请根据相关信息，解答下列问题：

（Ⅰ）填表：

离开学校的时间 $/h$	0.1	0.5	0.8	1	3
离学校的距离 $/\mathit{km}$	2	10		12

（Ⅱ）填空：

①书店到陈列馆的距离为 　　 $\mathit{km}$ ；

②李华在陈列馆参观学习的时间为 　　 $h$ ；

③李华从陈列馆回学校途中，减速前的骑行速度为 　　 $\mathit{km}/h$ ；

④当李华离学校的距离为 $4\mathit{km}$ 时，他离开学校的时间为 　　 $h$ ．

（Ⅲ）当 $0⩽x⩽1.5$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式．

将直线 $y=-6x$向下平移2个单位长度，平移后直线的解析式为 　　．

当自变量 $-1⩽x⩽3$时，函数 $y=|x-k|(k$为常数）的最小值为 $k+3$，则满足条件的 $k$的值为　　．

）已知正比例函数 $y=\mathit{kx}(k\ne 0)$ 与反比例函数 $y=\frac{6}{x}$ 的图象都经过点 $A(m,2)$ ．

（1）求 $k$ ， $m$ 的值；

（2）在图中画出正比例函数 $y=\mathit{kx}$ 的图象，并根据图象，写出正比例函数值大于反比例函数值时 $x$ 的取值范围．

某品牌鞋子的长度 $\mathit{ycm}$ 与鞋子的"码"数 $x$ 之间满足一次函数关系．若22码鞋子的长度为 $16\mathit{cm}$ ，44码鞋子的长度为 $27\mathit{cm}$ ，则38码鞋子的长度为 $($ 　　 $)$

A．

$23\mathit{cm}$

B．

$24\mathit{cm}$

C．

$25\mathit{cm}$

D．

$26\mathit{cm}$

如图，已知直线 $y=\mathit{kx}+b(k\ne 0)$与双曲线 $y=\frac{6}{x}$相交于 $A(m,3)$、 $B(3,n)$两点．

（1）求直线 $\mathit{AB}$的解析式；

（2）连结 $\mathit{AO}$并延长交双曲线于点 $C$，连结 $\mathit{BC}$交 $x$轴于点 $D$，连结 $\mathit{AD}$，求 $\mathit{\Delta ABD}$的面积．