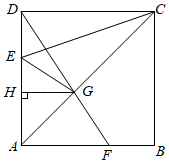
小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映了小明离家的距离 (单位: 与时间 (单位: 之间的对应关系.下列描述错误的是

| A. |
小明家距图书馆 |
| B. |
小明在图书馆阅读时间为 |
| C. |
小明在图书馆阅读书报和往返总时间不足 |
| D. |
小明去图书馆的速度比回家时的速度快 |
在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质及其应用的过程.以下是我们研究函数 的性质及其应用的部分过程,请按要求完成下列各小题.
(1)请把下表补充完整,并在给出的图中补全该函数的大致图象;
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
0 |
|
4 |
|
0 |
|
|
|
|
(2)请根据这个函数的图象,写出该函数的 条性质;
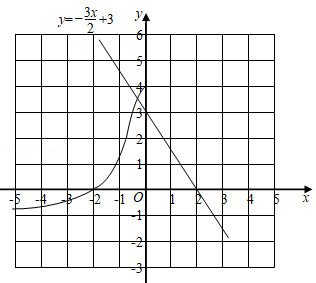
(3)已知函数 的图象如图所示.根据函数图象,直接写出不等式 的解集.(近似值保留一位小数,误差不超过
电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板上人的质量 之间的函数关系式为 (其中 , 为常数, ,其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻 的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为 ,该读数可以换算为人的质量 ,
温馨提示:①导体两端的电压 ,导体的电阻 ,通过导体的电流 ,满足关系式 ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压

(1)求 , 的值;
(2)求 关于 的函数解析式;
(3)用含 的代数式表示 ;
(4)若电压表量程为 伏,为保护电压表,请确定该电子体重秤可称的最大质量.
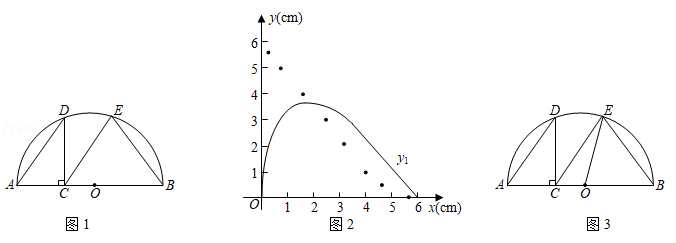
如图1,点 是半圆 的直径 上一动点(不包括端点), ,过点 作 交半圆于点 ,连结 ,过点 作 交半圆于点 ,连结 .牛牛想探究在点 运动过程中 与 的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量 变化的规律.
通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
|
|
|
0.30 |
0.80 |
1.60 |
2.40 |
3.20 |
4.00 |
4.80 |
5.60 |
|
|
|
|
2.01 |
2.98 |
3.46 |
3.33 |
2.83 |
2.11 |
1.27 |
0.38 |
|
|
|
|
5.60 |
4.95 |
3.95 |
2.96 |
2.06 |
1.24 |
0.57 |
0.10 |
|
(1)当 时, .
(2)在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.
(3)由(2)知" 取某值时,有 ".如图3,牛牛连结了 ,尝试通过计算 , 的长来验证这一结论,请你完成计算过程.
已知 , 两地相距 ,甲、乙两人沿同一条公路从 地出发到 地,甲骑自行车匀速行驶 到达,乙骑摩托车,比甲迟 出发,行至 处追上甲,停留半小时后继续以原速行驶.他们离开 地的路程 与甲行驶时间 的函数图象如图所示.当乙再次追上甲时距离 地

| A. |
|
B. |
|
C. |
|
D. |
|
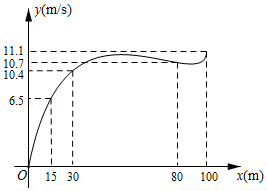
根据数学家凯勒的"百米赛跑数学模型",前30米称为"加速期",30米 米为"中途期",80米 米为"冲刺期".市田径队把运动员小斌某次百米跑训练时速度 与路程 之间的观测数据,绘制成曲线如图所示.
(1) 是关于 的函数吗?为什么?
(2)"加速期"结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
如图,在矩形 中, , .点 从点 出发,以 的速度在矩形的边上沿 运动,点 与点 重合时停止运动.设运动的时间为 (单位: , 的面积为 (单位: ,则 随 变化的函数图象大致为

| A. |
|
B. |
|
| C. |
|
D. |
|
在"看图说故事"活动中,某学习小组结合图象设计了一个问题情境.已知学校、书店、陈列馆依次在同一条直线上,书店离学校 ,陈列馆离学校 .李华从学校出发,匀速骑行 到达书店;在书店停留 后,匀速骑行 到达陈列馆;在陈列馆参观学习一段时间,然后回学校;回学校途中,匀速骑行 后减速,继续匀速骑行回到学校.给出的图象反映了这个过程中李华离学校的距离 与离开学校的时间 之间的对应关系.
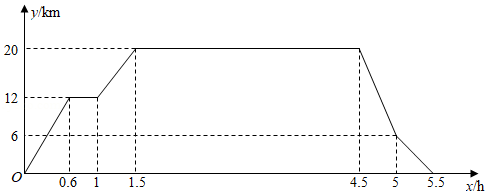
请根据相关信息,解答下列问题:
(Ⅰ)填表:
|
离开学校的时间 |
0.1 |
0.5 |
0.8 |
1 |
3 |
|
离学校的距离 |
2 |
10 |
|
12 |
|
(Ⅱ)填空:
①书店到陈列馆的距离为 ;
②李华在陈列馆参观学习的时间为 ;
③李华从陈列馆回学校途中,减速前的骑行速度为 ;
④当李华离学校的距离为 时,他离开学校的时间为 .
(Ⅲ)当 时,请直接写出 关于 的函数解析式.
函数图象是研究函数的重要工具。探究函数性质时,我们经历了列表、描点、连线画出函数图象,然后观察分析图象特征,概括函数性质的过程。请结合已有的学习经验,画出函数 的图象,并探究其性质.
列表如下:
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
(1)写出表中 、 的值,并在平面直角坐标系中画出该函数的图象;
(2)观察函数 的图象,判断下列关于该函数性质的命题:
①当 时,函数图象关于直线 对称;
② 时,函数有最小值,最小值为 ;
③ 时,函数 的值随 的增大而减小.
其中正确的是 .(请写出所有正确命题的番号)
(3)结合图象,请写出不等式 的解集 .

一对变量满足如图的函数关系.设计以下问题情境:
①小明从家骑车以600米 分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1000米 分的速度匀速骑回家.设所用时间为 分钟,离家的距离为 千米;
②有一个容积为1.5升的开口空瓶,小张以0.6升 秒的速度匀速向这个空瓶注水,注满后停止,等2秒后,再以1升 秒的速度匀速倒空瓶中的水.设所用时间为 秒,瓶内水的体积为 升;
③在矩形 中, , ,点 从点 出发.沿 路线运动至点 停止.设点 的运动路程为 , 的面积为 .
其中,符合图中函数关系的情境个数为

| A. |
3 |
B. |
2 |
C. |
1 |
D. |
0 |
如图,点 在正方形 边 上,点 是线段 上的动点(不与点 重合), 交 于点 , 于点 , , .
(1)求 ;
(2)设 , ,试探究 与 的函数关系式(写出 的取值范围);
(3)当 时,判断 与 的位置关系并说明理由.