高中数学代数拓展试题

已知 $\sin \alpha =\frac{\sqrt{5}}{5}$ ，且 $\alpha$ 是第一象限．
（1）求 $\tan (\pi +\alpha )+\frac{\sin \left({\displaystyle \frac{\mathrm{\pi }}{2}}-\alpha \right)}{\cos \left(\mathrm{\pi }-\mathrm{\alpha }\right)}$ 的值；
（2）求 $\tan (\alpha +\frac{\mathrm{\pi }}{4})$ 的值．

已知 $\theta$ 是第三象限角，且 ${\sin }^4\theta +{\cos }^4\theta =\frac{5}{9}$ ，那么 $\sin 2\theta$ = ．

sin的值是（）

A．

B．﹣

C．

D．

已知函数f（x）=sinx+cosx．
（1）若f（x）=2f（﹣x），求的值；
（2）求函数F（x）=f（x）•f（﹣x）+f²（x）的最大值和单调递增区间．

已知 $\sin \alpha =2\cos \alpha$ ，求 $\frac{\sin \alpha -4\cos \alpha }{5sin\alpha +2cos\alpha }$ 及 $\mathrm{si}{n}^2\alpha +2\sin \alpha \cos \alpha$ 的值．

如果sinα=，α∈（0，），那么cos（π﹣α）=（）

A．

B．

C．﹣

D．﹣

已知数列{a_n}的前n项和S_n，a₁=﹣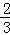，S_n+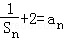（n≥2）．
（1）计算S₁，S₂，S₃，猜想S_n的表达式并用数学归纳法证明；
（2）设b_n=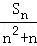，数列的{b_n}的前n项和为T_n，求证：T_n＞﹣．

已=2，则tanθ ．

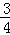若在定义域内存在实数x₀，使得f（x₀+1）=f（x₀）+f（1）成立，则称函数f（x）是“可拆函数”．
（1）函数f（x）=是否是“可拆函数”？请说明理由；
（2）若函数f（x）=2x+b+2^x是“可拆函数”，求实数b的取值范围：
（3）证明：f（x）=cosx是“可拆函数”．

若sinθ=，cosθ=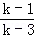，且θ的终边不落在坐标轴上，则tanθ的值为（）

A．	B．或0
C．0	D．以上答案都不对

已知f（α）=．
（1）化简f（α）；
（2）若角α终边上一点的坐标为（5a，12a），a≠0，求f（α）的值．

关于函数f（x）=4sin（2x+），（x∈R）有下列命题：
①y=f（x）是以2π为最小正周期的周期函数；
②y=f（x）可改写为y=4cos（2x﹣）；
③y=f（x）的图象关于点（﹣，0）对称；
④y=f（x）的图象关于直线x=对称；
其中正确的序号为 ．

符号表示不超过的最大整数，如，定义函数，那么下列结论中正确的序号是 ．
①函数的定义域为，值域为；
②方程有无数解；
③函数是周期函数；
④函数在是增函数．

给出下列四个等式：，，，，下列函数中不满足以上四个等式中的任何一个的是（）

A．	B．
C．	D．

设，那么的值为（）

A．

B．

C．

D．