高中数学初等数论初步试题

命题p：关于x的不等式x²+2ax+4＞0，对一切x∈R恒成立，命题q：指数函数f（x）=（3﹣2a）^x是增函数，若p∨q为真，p∧q为假，求实数a的取值范围．

命题“∃x∈R，e^x＜x”的否定是（）

A．∃x∈R，e^x＞x	B．∀x∈R，e^x≥x
C．∃x∈R，e^x≥x	D．∀x∈R，e^x＞x

函数f（x）=3ax﹣2a+1在[﹣1，1]上存在一个零点，则实数a的取值范围是（）

A．

B．a≤﹣1

C．

D．

下面式子正确的是（）

A．5^﹣0.2＞5^﹣0.1

B．lge＞lg3

C．0.1^0.8＜0.2^0.8

D．log3π＜log20.8

如图，直三棱柱ABC﹣A₁B₁C₁中，AC⊥BC，AC=BC=CC₁=2，M，N分别为AC，B₁C₁的中点．

（Ⅰ）求证：MN∥平面ABB₁A₁；
（Ⅱ）线段CC₁上是否存在点Q，使A₁B⊥平面MNQ？说明理由．

国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：

由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图：

（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s²=[（x₁﹣）²+（x₂﹣）²+…+（x_n﹣）²]，其中为数据x₁，x₂，…，x_n的平均数．）

为了了解学生的视力情况，随机抽查了一批学生的视力，将抽查结果绘制成频率分布直方图（如图所示）．若在[5.0，5.4]内的学生人数是2，则根据图中数据可得被样本数据在[3.8，4.2）内的人数是 ．

已知函数f（x）=x²+2x+alnx（a∈R）．
（1）当时a=﹣4时，求f（x）的最小值；
（2）若函数f（x）在区间（0，1）上为单调函数，求实数a的取值范围．

已知f（x）=﹣（x﹣1）²+m，g（x）=xe^x，若∃x₁，x₂∈R，使得f（x₁）≥g（x₂）成立，则实数m的取值范围是 ．

已知函数是偶函数．
（1）求k的值；
（2）若函数y=f（x）的图象与直线没有交点，求b的取值范围．
（3）设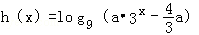，若函数f（x）与h（x）的图象有且只有一个公共点，求实数a的取值范围．

已知函数f（x）=，若存在实数a，b，c，d，满足f（a）=f（b）=f（c）=f（d），其中0＜a＜b＜c＜d，则abcd的取值范围 ．

若函数f（x）=x²+ax+1在（0，2）上有两个零点，则实数a的取值范围为 ．

已知函数y=f（x）是y=a^x（a＞0且a≠1）的反函数，且函数y=f（x）的图象过点（9，2），则a= ．

函数f（x）=e^x﹣x﹣2的零点所在的区间为（）

A．（﹣1，0）

B．（1，2）

C．（0，1）

D．（2，3）

定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M 成立，则称f（x）是D上的有界函数，其中M称为函f（x）的一个上界．已知函数f（x）=1+a+，g（x）=．
（1）若函数g（x）为奇函数，求实数a的值；
（2）在（1）的条件下，求函数g（x），在区间[，3]上的所有上界构成的集合；
（3）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．