初中物理速度公式及其应用计算题

严重的雾霾天气，对国计民生已造成严重的影响，其中，汽车尾气是形成雾霾的重要污染源。城市地铁列车可实现零排放，大力发展地铁，可以大大减少燃油汽车的使用，减少汽车尾气的排放。现有一沿直线运动的地铁列车，以恒定功率 $6\times {10}^3\mathit{kW}$从甲站由静止开始起动，先以 $36\mathit{km}/h$的平均速度加速运动 $20s$后，再以 $72\mathit{km}/h$的速度匀速运动 $80s$，接着关闭发动机，列车失去牵引力，以加速运动时的平均速度作减速运动，经过 $15s$后到达乙站停止。求：

（1）甲站到乙站的距离。

（2）牵引力做的功。

如图甲所示是使用汽车打捞水库中重物的示意图，汽车通过定滑轮牵引水下一个质量均匀分布的正方体重物，在整个打捞过程中，汽车以恒定的速度 $v=0.1m/s$向右运动。图乙是此过程中汽车拉力 $F$跟时间 $t$变化的图象。设 $t=0$时汽车开始提升重物，忽略水的阻力和滑轮的摩擦， $g$取 $10N/\mathit{kg}$。求：

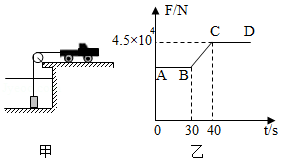
（1）水库水的深度；

（2）重物的密度。

（3）整个打捞过程中汽车的最小功率。

现代城市人口密度越来越大，交通越来越拥堵。易步车（如图甲）以其体积小巧，结构简洁和驱动安全等优点，成为短途出行的理想交通工具。某品牌易步车的部分参数如下表所示。质量为 $60\mathit{kg}$的雯雯从家骑行该品牌易步车上学（如图乙），以最大速度匀速行驶 $10\mathit{min}$到达学校，行驶中易步车所受阻力为人和车总重的0.1倍，设该过程中电机始终以额定功率工作。（取 $g=10N/\mathit{kg})$。求：

电池	$4\mathit{AH}$锂电池
电机额定功率	$500W$
最大速度	$18\mathit{km}/h$
单轮胎触地面积	$25c{m}^2$
轮胎个数	2
车身自重	$20\mathit{kg}$

（1）雯雯的家到学校的距离。

（2）雯雯在水平路面上骑易步车时，车对地面的压强。

（3）雯雯上学过程中，易步车电机的效率。

科技人员为了研究“物品均匀投放下水的方法”建立如图模型：轻质杠杆 $\mathit{AB}$两端用轻绳悬挂着两个完全相同的正方体物品甲和乙，甲、乙的边长均为 $a$，密度均为 $\rho (\rho$大于水的密度 ${\rho }_{水})$，杠杆放在可移动支点 $P$上，物品乙放在水平地面上。起初，物品甲下表面无限接近水面（刚好不被水打湿）。计时开始 $(t=0)$，上推活塞，使水面以速度 $v$匀速上升直到物品甲刚好完全被水淹没，停止计时（不计物品甲在水中相对运动的阻力）。上述过程中通过移动支点 $P$维持 $\mathit{BD}$绳中拉力恒为乙重力的0.6倍，且杠杆始终水平。 $(g$为已知量）

求：（1）物品乙对地面的压强；

       （2） $t=0$时， $\mathit{BP}:\mathit{PA}$为多少？

       （3）物品甲完全被水淹没时， $\mathit{BP}:\mathit{PA}$为多少？

       （4）任意时刻 $t$时， $\mathit{BP}:\mathit{PA}$与 $t$的关系式。

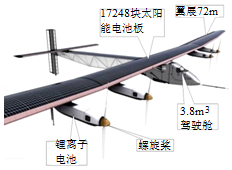
2015年3月9日，全球最大太阳能飞机“阳光动力2号”（如图所示）从阿联酋首都阿布扎比起程，开始环球飞行。将用时四到五个月穿越海洋陆地，完成人类史上首次太阳能环球飞行计划。“阳光动力2号”的机身和机翼均采用极轻的碳纤维材料。它的翼展达到 $72m$，比波音 $747-8$型的翼展还要宽 $3.5m$；机长 $22.4m$，接近一个篮球场的长度；而质量仅有 $2300\mathit{kg}$，跟一辆中型轿车相差无几。它的起飞速度为 $35\mathit{km}/h$，最大速度约 $140\mathit{km}/h$。“阳光动力2号”的机翼、机身和水平尾翼上共贴敷了17248片 $135\mathit{\mu m}$厚的单晶硅薄膜太阳能电池。这些电池可以产生最大 $70\mathit{kW}$的功率，这些电力可以输出给四台单台功率 $13.5\mathit{kW}$的电动机带动四扇 $4m$直径的双叶螺旋桨给飞机提供动力。“阳光动力2号”白天会爬升到 $9000m$的高度以避开气流并最大化利用太阳能，此时的温度急剧升高，而夜晚则半滑翔飞行，逐渐降低到 $1500m$高度，其速度并不大，因此夜里对能源的需求也大大减少。

（1）“阳光动力2号”的机身和机翼均采用极轻的碳纤维材料。“极轻”的物理含义是　        　。

（2）“阳光动力2号”吸收　     　能转化为电能，电能转化为飞机需要的其他形式能。

（3）在狭小的机舱内，两名瑞士飞行员将轮流驾驶，每次连续飞行5个昼夜，速度按 $80\mathit{km}/h$计算，每次连续飞行的距离是　      　 $\mathit{km}$。

（4）阳光动力2号从夜晚航行转为白天航行过程中，飞机的重力势能逐渐　     　。

科技改变生活，当今社会已步入汽车和微信时代。

（1）一辆质量为1500千克的某品牌汽车，静止在水平路面时，轮胎与地面接触的总面积为0.02米 ${}^2$，此时该汽车对路面的压强为　　帕。

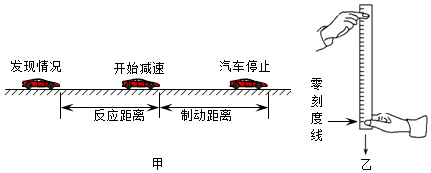
（2）若小柯在平直公路上以72千米 $/$小时的速度边看微信边匀速行车，当发现前方路面50米处有障碍物时，小柯在　　系统的调节下立即采取相应的刹车措施。据相关部门测定，司机正常反应时间约0.6秒，而边看微信边开车，反应时间会变为正常反应时间的3倍。该车以不同速度行驶时制动距离见下表。请结合表中数据及图甲，计算车子若按原运动方向行驶能否在撞上障碍物前停下。

速度（千米 $/$时）	制动距离（米 $)$
40	8
60	20
72	28

注：反应时间：司机从发现情况到操纵制动器所需要的时间；

反应距离：汽车在司机的反应时间里以原来速度行驶所通过的距离；

制动距离：当司机制动刹车后，汽车还会继续滑行的距离。

（3）人的反应时间的长短可通过图乙所示的方法进行比较：当竖直下落的直尺被捏住位置的刻度值越小（越靠近尺的下端），则说明反应时间　　。为了利用直尺定量测出人的反应时间，可在该直尺的另一面标记出表示反应时间的刻度线及对应刻度值，且每格代表的时间相等，则每格的长度是　　的（选填“相等”或“不相等” $)$。（不计空气阻力）

如图所示，是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图，已知井深 $10m$，物体重 $G=4\times {10}^{3}N$，汽车重 $G_{车}=3\times {10}^{4}N$，汽车匀速拉绳子时的拉力 $F=2\times {10}^{3}N$，汽车受到的阻力为车重的0.05倍。请计算：

（1）若汽车运动的速度为 $1.2m/s$，则将物体由井底拉至井口，需要多长时间？

（2）滑轮组的机械效率是多少？（保留一位小数）

（3）汽车的牵引力是多大？

（4）将物体由井底拉至井口，汽车的牵引力做的功是多少？

小华家新买了电动自行车，说明书上的部分内容录在如图甲中（注：“电池容量 $10\mathit{Ah}$”可理解为“若以10安的电流放电可使用1小时” $)$。请回答：

（1）该电动自行车的额定电流多大？

（2）若该电动自行车行驶的平均车速为20千米 $/$时，使用 $50\%$的电池容量（按额定电流放电，不计放电时能量损失），能行驶多长路程？

（3）某天小华想在自家的小车库内充电，发现车库内只安装了电灯，没有插座，于是小华想在如图乙所示的原有线路上安装一个双孔插座，应在 $a$、 $b$、 $C$三处中哪两处之间安装才合理？　　。

$A$． $a$和 $b$    $B$． $b$和 $c$     $C$． $a$和 $c$

电动车是环保的交通工具，行驶时蓄电池给电动机供电，表1是某厂家生产的电动车的主要参数，测试员还做了其他参数的测试。

测试一：一次性充满电后，在相同的路面、不同负重情况下连续行驶的最大里程数s_m，结果如表2。

表1：

整车	整车质量	40kg
	最高车速	30km/h
蓄电池	蓄电容量	0.55kW•h
电动机	额定电压	48V
	额定功率	240W

表2：

负重（kg）	60	80	100	120
sm（km）	28	25.8	23.3	20.5

测试二：电动车一次性充满电后连续行驶直至储存电能将耗尽的过程中，在同样的路面，行驶里程s对电动机牵引力F的影响，得到的图象如图所示。

根据以上数据求：

（1）电动车以6m/s速度匀速行驶100s的路程。

（2）由表2数据反映的现象，其原因是　　。

（3）在测试二中电动车的蓄电池所储存的能量剩余量低于10%后电动车已无法连续行驶，此时行驶里程为30km，求这次测试中该电动车的效率。

小安和小锋检修自行车时观察到：摇动自行车脚踏板时，大齿轮转动并通过链条带动小齿轮一起转动。小锋认为两齿轮转动一样快，小安则认为小齿轮比大齿轮快，两人带着不同的观点请教老师。

老师解释道：你们说的都有些道理，此轮转动时，其周边的齿轮绕轴心作轨迹为圆的运动﹣﹣圆周运动，可以通过轮齿的运动来研究齿轮的转动，比较物体做圆周运动的快慢有两种方法：①比较单位时间内物体通过的圆弧长，物理学中称为线速度，计算公式 $v=\frac{s}{t}$（v：线速度 s：圆弧长 t：时间）；②比较单位时间内物体与圆心连线（半径）扫过的角度（如图甲所示），物理学中称为角速度，用字母Ω表示，国际单位是弧度/秒（rad/s）二者之间的关系满足公式：v＝Ωr，r表示圆的半径，要比较齿轮转动的快慢，就需要判断大，小齿轮上的轮齿在运动过程中各物理量的大小。

根据老师的解释，请你解答下列问题：

（1）如图乙所示，匀速摇动脚踏板时，大齿轮上某个轮齿（标记为a）在1s内从A点运动到A′点，弧长 $\stackrel{̂}{A{A}^{\text{'}}}$＝0.16m，则轮齿a的线速度v是多大？

（2）若轮齿a到轴心的距离r₀＝0.1m，其角速度ϖ是多大？

（3）A点与轴心的连线上有一点C，请你根据角速度的定义判断齿轮转动过程中A，C两点角速度的大小关系，并说明理由。

（4）小齿轮上的某个轮齿（标记为b），在轮齿a由A点运动到A′点的同时从B点运动到B′点，弧长为 $\stackrel{̂}{B{B}^{\text{'}}}$，测量发现 $\stackrel{̂}{B{B}^{\text{'}}}$＝ $\stackrel{̂}{A{A}^{\text{'}}}$．请你结合上述材料分别解释两位同学的观点。（链条长度固定且运动过程中与齿轮不打滑）

在一次车辆故障处置过程中，拖车所用装置简化如图。为了尽快疏通道路，交警只用了30s的时间，指挥拖车在水平路面上将质量是1.5t的故障车匀速拖离了现场。若故障车被拖离的速度是6m/s，绳子自由端的拉力F是500N，该装置的机械效率是80%．求：

（1）故障车在30s内通过的路程；

（2）拉力F在30s内所做的功；

（3）故障车在被拖离过程中受到的阻力。

一辆重2×10⁴N的卡车，开进了一段泥泞的道路，不能继续行驶．司机找来一辆小型拖拉机、绳子、动滑轮，采用如图所示装置，拖拉机在绳端用3750N的水平拉力，将汽车以0.2m/s的速度水平匀速拉出泥泞路段，用时10s．

（1）卡车移动的距离。
（2）求拉力F做的功和功率．
（3）若动滑轮的机械效率为80%，求汽车所受的阻力．

一列火车长200m,以40m/s的速度通过长1800m的大桥,求火车过桥所用的时间?

汽车从A站出发,以90km/h的速度行驶了20min后到达B站,又以60km/h的速度行驶了10min到达C站,问（1）AB两站相距多远？（2）汽车从A站到C站的平均速度？

寒假里，小刚乘火车去外婆家时，观察到他乘坐的火车共有12节车厢（包括火车头），已知每节车厢长15m，当火车以72km/h的速度匀速穿过一条隧道时，他测出自己通过隧道的时间为80s。求：
（1）该火车有多长？
（2）此隧道多长？
（3）火车完全通过隧道需要多长时间？