初中物理运动和力计算题

汽车出厂前要进行测试．某次测试中，先让汽车在模拟山路上以8m/s的速度行驶500s，紧接着在模拟公路上以20m/s的速度行驶100s．求：
（1）该汽车在模拟山路上行驶的路程；
（2）汽车在这次整个测试中的平均速度．

被誉为“中国豹”的国产主站99式坦克，其相关性能数据如表所示．

质量	54t
成员	3﹣4人
单条履带的触地面积	1.8m^2
发动机功率	1100kW
最大越野时速	60km/h
基本作战行程	450km

在某次野战训练中，该坦克接到命令，距它30km处发现“敌情”．取g=10N/kg，通过计算回答：
（1）该坦克到达目的地最快需要多长时间？
（2）该坦克在赶往目的地的过程中，发动机做了多少功？
（3）该坦克对水平地面的压强多大？

邵坪高速是连接邵阳市与新邵坪上沪昆高铁站的重要交通线，全长约34km，预计于今年年底正式通车．通车后，邵坪高速将与沪昆高铁实现无缝对接，有望实现1h左右从邵阳抵达长沙．若一辆小车质量为1.5×10³kg，每个车轮与路面的接触面积为0.15m²，如图所示，请计算（g取10N/kg）：

（1）该小车的重力为多少N？
（2）该小车静止在水平路面上对路面的压强为多少Pa？
（3）若邵坪高速限速100km/h，该小车驶完邵坪高速全程最少需多少h？

汽车发动机效率η是指发动机牵引汽车前进所做的功与汽油完全燃烧产生内能的比值，一辆小汽车在高速公路上匀速行驶200km，所用时间是2h，消耗汽油14L（汽油完全燃烧），若此汽车汽油发动机的效率η是25%，汽油密度ρ_汽油=0.8×10³kg/m³，汽油热值q_汽油=4.5×10⁷J/kg。

（1）求该汽车在高速公路上行驶这段时间内的牵引力和牵引力功率的大小。
（2）汽车驶出高速公路后，进入某国道，如图为此国道某直线路段的一处测速仪，测速仪内有能发射和接受超声波的传感器。在汽车以某一速度v远离测速仪某段距离L＝64m时，测速仪发出超声波经汽车反射后接收到超声波信号的时间为0.4s。已知此路段限速为80km/h，超声波的速度为340m/s。试计算并说明汽车在此路段是否超速？

电梯是高层住宅必备的交通工具。如图甲所示是某种升降电梯工作原理图，它由轿厢、对重、电动机、钢丝绳、滑轮等部件连接组成，电动机和对重通过钢丝绳分别给轿厢施加拉力，连接轿厢的两根钢丝绳非常靠近，轿厢与对重的运动方向始终相反。对重的质量为400kg，空轿厢的质量是500kg，额定载重量是1000kg。某次电梯满载上升时的v一t图像如图乙所示。不计钢丝绳重力和一切摩擦。(g="10" N／kg)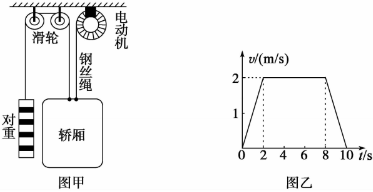

(1)电梯匀速上升的高度是多少？
(2)电梯匀速运动阶段，对重的重力做的功是多少？
(3)电梯匀速运动时，电动机钢丝绳对轿厢拉力的功率是多少？
(4)简述对重的作用。（至少两条）

一辆汽车行驶在平直公路上，总重为1.2×10⁴N，轮胎与地面总接触面积为0.12m²，该车30min内匀速行驶了30km，消耗汽油4kg，汽油完全燃烧放出的热量有30%转化为机械能．（汽油的热值为4.6×10 ⁷J/kg）求该汽车：
（1）匀速行驶的速度；
（2）静止在水平路面上时，对路面的压强是多少？
（3）这段时间内获得的机械能．

有一根绳子，通过如图19甲所示的滑轮组，能够提起的最重的物体是A，物体再重绳子将断裂（不计绳重和摩擦）。求：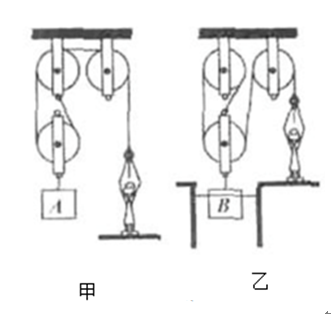

（1）将A匀速提高2m做的有用功为740J，则物重G_A为多少？
（2）若此时滑轮组机械效率为92.5%，人的体重为600N，每只脚与地的接触面积为2×10^-2m²，则人对地面压强为多少？绳子能承受的最大拉力为多少？
（3）若利用这根绳子和这些滑轮，组成图19乙所示滑轮组，利用它从水中缓慢提起（不计水的阻力）一个边长为3×10^-1m的正方体B，当提到B的下表面所受水的压强为2×10³Pa时绳子断裂。则正方体B的密度为多少？

匀速直线运动是指在任何相等的时间内通过相等路程的直线运动，匀加速直线运动是指在任何相等的时间内增加相同速度的直线运动，如从静止开始，1秒末的速度是2米/秒，则2秒末的速度是4米/秒．3秒末的速度是6米/秒……
作匀速直线运动的物体在时间t内移动的距离s=vt，在它的v—t图象中（下图1），阴影矩形的边长正好是v和t，可见，做匀速直线运动的物体移动的距离对应着v—t图象中阴影的面积，匀加速直线运动的物体移动的距离也有类似的关系。
现有一辆汽车在教练场上由静止开始沿平直道路做匀加速运动，在10秒末速度达到 10米/秒．然后以此速度做50秒的匀速直线运动，最后减速慢慢停下。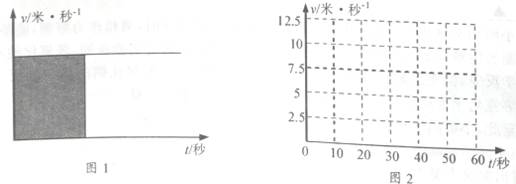

（1）从汽车由静止开始运动计时，在下图2中做出汽车在1分钟内的v—t图象。
（2）求这1分钟内汽车行驶的距离。
（3）汽车在行驶的过程中，在水平方向上受到使汽车前进的牵引力F₁和阻碍汽车运动的阻力F₂，试分析这一分钟内F₁和F₂的大小关系。

如图所示，一轻绳绕过定滑轮，一端与粗糙水平面上的滑块相连，另一端悬挂一个砂桶。调整桶内砂的质量，当砂桶和砂的总质量m=0.2kg时，砂桶和滑块都做匀速直线运动，速度大小v=0.5m/s，不计滑轮的摩擦，求砂桶和滑块匀速运动时：

（1）滑块受到的摩擦力的大小；
（2）砂桶和砂所受的重力在2s内做的功。

图1—5—13（a），在天平左盘放一杯水，右盘放砝码，使天平平衡．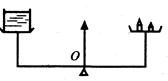
　　
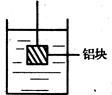
（a）　　　　　　　（b）
图1—5—13
　　（1）将一质量为27g的铝块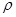（_铝＝2.7g/m³）放入左盘水中，水不溢出，天平还能平衡吗？
　　（2）将铝块如图1—5—13（b）方式放入左盘中，天平还能平衡吗？

电动车是环保的交通工具，行驶时蓄电池给电动机供电，表1是某厂家生产的电动车的主要参数，测试员还做了其他参数的测试。

测试一：一次性充满电后，在相同的路面、不同负重情况下连续行驶的最大里程数s_m，结果如表2。

表1：

整车	整车质量	40kg
	最高车速	30km/h
蓄电池	蓄电容量	0.55kW•h
电动机	额定电压	48V
	额定功率	240W

表2：

负重（kg）	60	80	100	120
sm（km）	28	25.8	23.3	20.5

测试二：电动车一次性充满电后连续行驶直至储存电能将耗尽的过程中，在同样的路面，行驶里程s对电动机牵引力F的影响，得到的图象如图所示。

根据以上数据求：

（1）电动车以6m/s速度匀速行驶100s的路程。

（2）由表2数据反映的现象，其原因是　　。

（3）在测试二中电动车的蓄电池所储存的能量剩余量低于10%后电动车已无法连续行驶，此时行驶里程为30km，求这次测试中该电动车的效率。

如图所示，某科技小组的同学制作了一个打捞物体的自动控制模型，E为配重，AOB是一个质地均匀的长方形横杆，其质量不计，OA∶OB=1∶3，在水平位置保持平衡。通过电动机Q可以控制杠杆B端抬起，从而将被打捞物体提起。已知滑轮D重为10N，B端定滑轮和提升电动机P的总质量是1kg，提升电动机P的功率为3W且保持不变，物体M的质量是1kg。只让提升电动机P工作，当物体M匀速上升时，提升电动机P对绳子的拉力为F₁， B端滑轮组的机械效率为η₁。若用质量为1.5kg物体N代替物体M，只让提升电动机P工作，当物体N匀速上升时，提升电动机P对绳子的拉力为F₂， B端滑轮组的机械效率为η₂，且η₁∶η₂=8∶9。不计绳的质量，不计滑轮与轴的摩擦,g取10N/kg，求：
（1）F₁与F₂的比值；
（2）只让提升电动机P工作，当物体M匀速上升时的速度υ；
（3）当物体N被提升到一定高度后，提升电动机P停止工作，启动电动机Q将杠杆B端匀速抬起的过程中，电动机Q对绳子的拉力F的大小。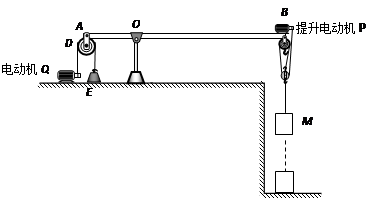

如图是一个上肢力量健身器示意图。配重A的底面积为5×10^-2m²，放在地面上对地面的压强P₀为2×10⁴Pa。B、C都是定滑轮，D是动滑轮；杠杆EH可绕O点在竖直平面内转动，OE∶OH=3∶5。小成受到的重力为500N，他通过细绳在H点施加竖直向下的拉力为T₁时，杠杆在水平位置平衡，小成对地面的压力为F₁，配重A受到的拉力为F_A1，配重A对地面的压强P₁为8×10³ Pa。小成在H点施加竖直向下的拉力为T₂时，杠杆仍在水平位置平衡，小成对地面的压力为F₂，配重A受到的拉力为F_A2，配重A对地面的压强P₂为6×10³Pa。已知F₁∶F₂=18∶17，杠杆EH和细绳的质量均忽略不计。

求：
（1）配重A受到的重力G_A；
（2）拉力T₁；
（3）动滑轮D受到的重力G。

早在1800年前的汉代，科学家张衡就发明了用来测量车辆行驶里程的“记里鼓车”，又名“记里车”、“司里车”、“大章车”等。科技史学家王振铎先生根据史书上的文字描述，复原了这种神奇的车，如图9甲所示。图9乙所示为记里鼓车的原理图，马匹拉着该车向前行走，带动左、右足轮转动。立轮与左、右足轮装在同一水平轴上，齿数为18，并与下平轮啮合，带动下平轮水平转动，下平轮齿数为54；齿数为3的旋风轮与下平轮装在同一竖轴上，并与中平轮啮合。中平轮齿数为100，转动一圈，轮上的拨子便拨动上层木人右臂击鼓一次，显示车行一里。

汉代曾以六尺为一步，三百步为一里，假设那时人们认为的圆周率约为3。试通过计算说明，这架“记里鼓车”的足轮直径应该是多少尺?

小安和小锋检修自行车时观察到：摇动自行车脚踏板时，大齿轮转动并通过链条带动小齿轮一起转动。小锋认为两齿轮转动一样快，小安则认为小齿轮比大齿轮快，两人带着不同的观点请教老师。

老师解释道：你们说的都有些道理，此轮转动时，其周边的齿轮绕轴心作轨迹为圆的运动﹣﹣圆周运动，可以通过轮齿的运动来研究齿轮的转动，比较物体做圆周运动的快慢有两种方法：①比较单位时间内物体通过的圆弧长，物理学中称为线速度，计算公式 $v=\frac{s}{t}$（v：线速度 s：圆弧长 t：时间）；②比较单位时间内物体与圆心连线（半径）扫过的角度（如图甲所示），物理学中称为角速度，用字母Ω表示，国际单位是弧度/秒（rad/s）二者之间的关系满足公式：v＝Ωr，r表示圆的半径，要比较齿轮转动的快慢，就需要判断大，小齿轮上的轮齿在运动过程中各物理量的大小。

根据老师的解释，请你解答下列问题：

（1）如图乙所示，匀速摇动脚踏板时，大齿轮上某个轮齿（标记为a）在1s内从A点运动到A′点，弧长 $\stackrel{̂}{A{A}^{\text{'}}}$＝0.16m，则轮齿a的线速度v是多大？

（2）若轮齿a到轴心的距离r₀＝0.1m，其角速度ϖ是多大？

（3）A点与轴心的连线上有一点C，请你根据角速度的定义判断齿轮转动过程中A，C两点角速度的大小关系，并说明理由。

（4）小齿轮上的某个轮齿（标记为b），在轮齿a由A点运动到A′点的同时从B点运动到B′点，弧长为 $\stackrel{̂}{B{B}^{\text{'}}}$，测量发现 $\stackrel{̂}{B{B}^{\text{'}}}$＝ $\stackrel{̂}{A{A}^{\text{'}}}$．请你结合上述材料分别解释两位同学的观点。（链条长度固定且运动过程中与齿轮不打滑）