初中物理物态变化计算题

如图所示，金属圆柱体甲的高度为d，底面积为S；薄壁圆柱形容器乙的底面积为2S，且足够高，其中盛有深度为H（H＞d）的液体，置于水平面上。
①若甲的体积为1×10^（3米³，密度为2×10³千克/米³，求它的质量m。
②若乙所受重力为G₁，其中所装液体重为G₂，求乙对水平面的压强p。
③现将甲浸入乙的液体中，其下表面所处深度为h，求液体对甲下表面压强p_甲与液体对乙底部压强p_乙的比值及其对应h的取值范围。

如图所示，正方体甲的边长为0.1米，密度为5×10³千克/米³，正方体乙的边长为0.2米，质量为24千克。

①求正方体乙的密度；
②求正方体乙对水平地面的压强；
③若沿正方体乙的上表面挖去一底面积为0.01米²、高为h的长方体，并在挖去部分中倒满水或酒精，是否有可能使甲、乙两物体对地面的压强相等（酒精密度0.8×10³千克/米³）？请通过计算做出判断。

体积为30cm³的空心铜球，它的质量为89g，现在用某种金属注满它的空心部分后球的质量变为245g．求这种金属的密度是多少？（ρ_铜=8.9×10³kg/m³）

某人用绳子将一物体从水面下2m深处的地方匀速提到水面0.5m处的过程中，人对物体做功为54J．当将物体拉到有体积露出水面时，让其静止，此时绳子对物体的拉力为40N．不计绳子的质量，忽略水的阻力，求物体的密度．（g取10N/kg）

如图所示轻质杠杆，把密度均为4.0×10³kg/m³的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的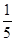，求：甲、乙两个物体的质量之比．

自制潜水艇模型如图所示，A为厚壁玻璃广口瓶，瓶的容积是V₀，B为软木塞，C为排水管，D为进气细管，正为圆柱形盛水容器．当
瓶中空气的体积为V₁时，潜水艇模型可以停在液面下任何深处，若通过细管D向瓶中压入空气，潜水艇模型上浮，当瓶中空气的体积为2 V_l时，潜水艇模型恰好有一半的体积露出水面，水的密度为恰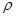_水 ，软木塞B，细管C、D的体积和重以及瓶中的空气重都不计．

求：（1）潜水艇模型的体积；
（2）广口瓶玻璃的密度．

底面积为400cm²的圆柱形容器内装有适量的水，将其竖直放在水平桌面上，把边长为10cm的正方体木块A放入水后，再在木块A的上方放一物体B，物体B恰好没入水中，如图1—5—11（a）所示．已知物体B的密度为6×10³kg/m³．质量为0.6kg．（取g＝10N/kg）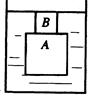

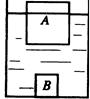
（a）        （b）
求：（1）木块A的密度．
（2）若将B放入水中，如图（b）所示，求水对容器底部压强的变化．

如图所示的木块浸没在水中，细线对木块的拉力是2N．剪断细线，待木块静止后，将木块露出水面的部分切去，再在剩余的木块上加1N向下的压力时，木块有20cm³的体积露出水面．求木块的密度．（g取10N/kg）

下图是我国设计的北京2008年奥运会奖牌，奖牌正面为国际奥委会统一规定的图案，奖牌背面镶嵌着取自中国的玉石，形象诠释了中华民族自古以来以“玉”比“德”的价值观，是中华文明与奥林匹克精神的一次“中西合璧”。奖牌分为金牌、银牌和铜牌。其中金牌由纯银、玉石、纯金组成，金牌的总体积约为23 cm³，镶嵌玉石的体积约为5.4cm ³，纯金的质量约为6g。（已知：ρ_玉=3.0g/cm³，ρ_金=19.3g/cm³，ρ_银="10.5" g/cm³）。请问：

(1)一枚金牌约需要玉石多少克？
(2)一枚金牌除了玉石和纯金外，还需纯银约多少克？（计算结果保留一位小数）

如图所示为FDP30C型柴油水泵机组（水泵机组动力由柴油机提供），它的优点是重量轻、体积小、功率大；省时、省油、省心．该水泵机组的效率为40%，正常工作1小时可以将54m³的水抽到20m高处，请计算这个过程中：（g=10N/kg，q_柴油=4.3×10⁷J/kg）．

（1）水泵机组对水做了多少功？
（2）水泵机组的有用功功率是多少？
（3）水泵机组消耗多少柴油？（结果保留两位小数）

如图所示，在台秤上放一个容器，容器内盛有适量水，弹簧秤下悬挂一个边长为10cm的正方体金属块，金属块的密度为3×10³kg/m³．

（1）金属块的重力．
（2）用弹簧测力计拉着金属块缓慢地下降，当金属块浸入水中4cm而未触及容器底部时，弹簧秤的示数为多少？
（3）金属块缓慢下降直至浸没但未触及容器底部的过程中，台秤示数是如何变化的？（整个过程中水不溢出）

如图是一种老式电饭锅的筒化电路原理图，该锅的部分参数如下表，煮饭时，温控开关S是闭合的，饭熟后，锅内温度达到103℃时，温控开关S自动断开，电饭锅转入保温状态．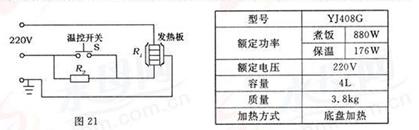

（1）在通常情况下用这种电饭锅烧水，开关S的自动断电功能不起作用，这是为什么？
（2）发热板R₁的阻值是多少？
（3）保温时，发热板的发热功率是多少？
（4）从能量利用率的角度计算说明这种电饭锅的不合理性．

18g水的体积是18㎝³，请通过计算，说明这些水结成冰后，体积怎样变化。（ρ_冰=0.9×10³㎏/m³）             

一个空瓶质量为300g，装满水后的总质量为800g；若向空瓶内装一些金属粒，测得瓶和金属粒的总质量为543g；然后往瓶中装满水，三者总质量为953g，求金属粒的密度。

利用轮船上的电动机和缆绳从水库底竖直打捞出一长方体物体，下图P-t图像中表示了电动机输出的机械功率P与物体上升时间t的关系。已知0～80s时间内，物体始终以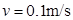的速度匀速上升，当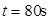时，物体底部恰好平稳的放在轮船的水平甲板上。已知电动机的电压是200V，物体上升过程中的摩擦阻力不计，g取10N/kg。求：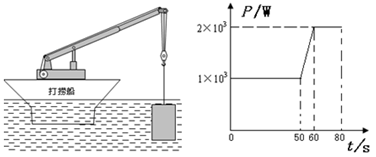

（1）湖水的深度h₁，甲板离水面距离h₂ 。
（2）物体的质量m，长度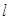，体积V 。
（3）若电动机电能转换为机械能的效率为80%，求在0～50s内，电动机线圈中电流的大小。