初中数学填空题

一天24小时中分针与时针垂直共有        次。

Δ○□○Δ○□○Δ○□○…左起第30个是_____.

如图，直线，点坐标为（1，0），过点作轴的垂线交直线于点，以原点为圆心，长为半径画弧交轴于点；再过点作轴的垂线交直线于点 ，以原点为圆心，长为半径画弧交轴于点，…，按此做法进行下去，点 的坐标为        ．

如图，四边形ABHK是边长为6的正方形，点C、D在边AB上，且AC=DB=1，点P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP，E、F分别为MN、QR的中点，连接EF，设EF的中点为G，则当点P从点C运动到点D时，点G移动的路径长为         

如图，正方形ABCD的对角线相交于点O，正三角形OEF绕点O旋转．在旋转过程中，当AE＝BF时，∠AOE的大小是________．

如图，边长为1的菱形ABCD中，∠DAB＝60°．连接对角线AC，以AC为边作第二个菱形ACEF，使∠FAC＝60°．连接AE，再以AE为边作第三个菱形AEGH，使∠HAE＝60°……按此规律所作的第n个菱形的边长是________．

如图，平面直角坐标系xOy中，点A、B的坐标分别为（3，0）、（2，－3），△AB′O′是△ABO关于点A的位似图形，且O′的坐标为（－1，0），则点B′的坐标为________．

把标准纸一次又一次对开，可以得到形状均相似的“开纸”．现在我们在长为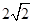、宽为1的矩形纸片中画两个小矩形，使这两个小矩形的每条边都与原矩形纸的边平行或小矩形的边在原矩形的边上，且每个小矩形均与原矩形纸相似，然后将它们剪下，则所剪得的两个小矩形纸片周长之和的最大值是________．

如图，在梯形ABCD中，AD∥BC，BE平分∠ABC交CD于E，且BE⊥CD，CE︰ED＝2︰1．如果△BEC的面积为2，那么四边形ABED的面积是________．

如图，直角三角形ABC中，∠ACB＝90°，AB＝10，BC＝6，在线段AB上取一点D，作DF⊥AB交AC于点F，现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为A₁；AD的中点E的对应点记为E₁．若△E₁FA₁∽△E₁BF，则AD＝________．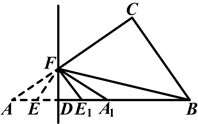

如图，在△ABC中，点D、E分别是边AB、AC的中点，DF过EC的中点G并与BC的延长线交于点F，BE与DF交于点O．若△ADE的面积为S，则四边形BOGC的面积＝________．

如图，点A，B的坐标分别是（0，8），（6，0），过边OA上的点P（0，4）作直线PQ与△OAB的另一边相交于点Q，当点Q的坐标为________时，形成的新三角形与△OAB相似．

如图，OABC是平行四边形，对角线OB在y轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线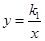和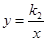的一个分支上，分别过点A、C作x轴的垂线，垂足分别为M、N，有以下的结论：
①；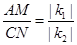
②阴影部分的面积是；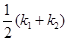
③当∠AOC＝90°时，|k₁|＝|k₂|；
④若OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．
其中正确的结论是________(把所有正确结论的序号都填上)．

已知P₁(x₁，y₁)，P₂(x₂，y₂)是同一个反比例函数图象上的两点，若x₂＝x₁＋2．且，则这个反比例函数的表达式为________．

如图，在x轴的正半轴上依次间隔相等的距离取点A₁，A₂，A₃，A₄，…，A_n，分别过这些点作x轴的垂线与反比例函数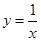的图象相交于点P₁，P₂，P₃，P₄，…，P_n，作P₂B₁⊥A₁P₁，P₃B₂⊥A₂P₂，P₄B₃⊥A₃P₃，P₅B₄⊥A₄P₄，…，P_nB_n－1⊥A_n－1P_n－1，垂足分别为B₁，B₂，B₃，B₄，…，B_n－1，连接P₁P₂，P₂P₃，P₃P₄，…，P_n－1P_n，得到一组Rt△P₁B₁P₂，Rt△P₂B₂P₃，Rt△P₃B₃P₄，…，Rt△P_n－1B_n－1P_n，则Rt△P_n－1B_n－1P_n的面积为________．