初中数学填空题

如图，在△ABC中，E，F分别是AC，BC边上的点，P₁，P₂，P₃，…，P_n−1是AB边的n等分点，CE = AC，CF = BC，∠B = 40°，AB = BC，则∠EP₁F +∠EP₂F +∠EP₃F + … +∠EP _n−1F = ________．

在直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若，则称点Q为点P的“可控变点”．       
例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．
（1）若点（﹣1，﹣2）是一次函数y=x+3图象上点M的“可控变点”，则点M的坐标为                ；（2）若点P在函数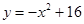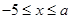（）的图象上，其“可控变点”Q的纵坐标y′的取值范围是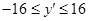，则实数a的取值范围是              ．

二次函数y=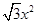的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y=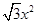的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积为      ．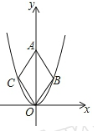

如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ=CE时，EP+BP=            ．

探索规律观察下面由※组成的图案和算式，解答问题

（1）请计算1+3+5+7+9+11=__________；
（2）请猜想1+3+5+7+9+…+19=__________；
（3）请猜想1+3+5+7+9+…+（2n﹣1）=__________；
（4）请用上述规律计算：21+23+25+…+99．

如图，直线y＝x－2与x轴、y轴分别交于M、N两点，现有半径为1的动圆圆心位于原点处，并以每秒1个单位的速度向右作平移运动．已知动圆在移动过程中与直线MN有公共点产生，当第一次出现公共点到最后一次出现公共点，这样一次过程中该动圆一共移动    秒．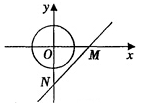

如图，在矩形ABCD中，AB=4，AD=10．连接BD，∠DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△BC′E′．当射线BE′和射线BC′都与线段AD相交时，设交点分别为F，G．若△BFD为等腰三角形，则线段DG长为        ．

如图，在△ABC中，AB＝AC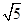＝，BC＝2，在BC上有100个不同的点P₁、P₂、P₃…P₁₀₀（BC中点除外），过这100个点分别作△ABC的内接矩形P₁E₁F₁G₁，P₂E₂F₂G₂…P₁₀₀E₁₀₀F₁₀₀G₁₀₀，设每个内接矩形的周长分别为L₁、L₂…L₁₀₀，则L₁＋L₂＋…＋L₁₀₀＝    ．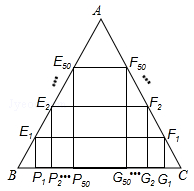

将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是             cm²．

若，则=      ．

AD为△ABC的中线，G为△ABC的重心，若=2，则=      ．

在反比例函数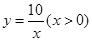的图象上，有一系列点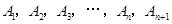，若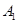的横坐标为2，且以后每点的横坐标与它前一个点的横坐标的差都为2，现分别过点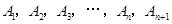，作x轴与y轴的垂线段，构成若干个矩形如下图所示，将图中阴影部分的面积从左到右依次记为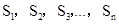，则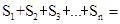______．（用n的代数式表示）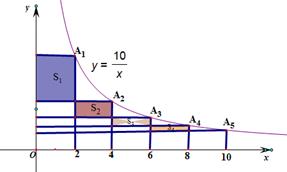

（本题12分）意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为正方形的边长值构造正方形：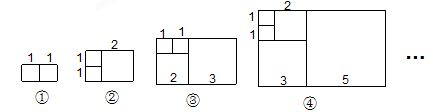

再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、 …相应长方形的周长如下表所示：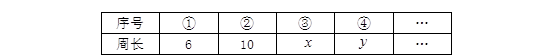

仔细观察图形，上表中的x=             ，y=            ．
若按此规律继续作长方形，则序号为⑧的长方形周长是               ．

一段抛物线，记为，它与x轴交于点O，，将绕点旋转
180°得，交x 轴于点；将绕点旋转180°得C3，交x 轴于点；……如此进行下去，直至
得．若P（2015，m）在第672段抛物线上，则m =       ．

如图，△ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作；取BE边中点，作∥FB，∥EF，得到四边形，它的面积记作．照此规律作下去，则=                ．