如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，连接DE、BF．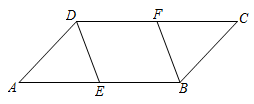
求证：△ADE≌△CBF．
如图，已知抛物线y=ax2+bx+c（a≠0）交x轴于A（﹣1，0），B（5，0）两点，与y轴交于点C（0，2）
（1）求抛物线的解析式；
（2）若点M为抛物线的顶点，连接BC、CM、BM，求△BCM的面积；
（3）连接AC，在x轴上是否存在点P使△ACP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
在平面直角坐标系中，点A的坐标是（0，3），点B的坐标是
，
（1）将△AOB绕点A逆时针旋转90°得到△AEF，点O，B对应点分别是E，F，请在图中画出△AEF；
（2）将线段AF绕点O旋转180°得到线段MN，点A、F对应点分别是M、N，请画出线段MN，并连结NF，直接写出线段NF的长
某商场购进一批单价为16元的日用品．若按每件23元的价格销售，每月能卖出270件；若按每件28元的价格销售，每月能卖出120件；若规定售价不得低于23元，假定每月销售件数y（件）与价格x（元/件）之间满足一次函数．
（1）试求y与x之间的函数关系式．
（2）在商品不积压且不考虑其他因素的条件下，销售价格定为多少时，才能使每月的毛利润w最大？每月的最大毛利润为多少？
（3）若要使某月的毛利润为1800元，售价应定为多少元？
如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA为半径的⊙O经过点D。
（1）求证：BC是⊙O切线；
（2）若BD=5，DC=3，求AC的长。
某汽车销售公司2013年盈利1500万元，到2015年盈利2160万元，且从2013年到2015年，每年盈利的年增长率相同．
（1）该公司2013年至2015年盈利的年增长率?
（2）若该公司盈利的年增长率继续保持不变，预计2016年盈利多少万元?
近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO．在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4 mg/L，此后浓度呈直线型增加，在第7小时达到最高值46 mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降．如图，根据题中相关信息回答下列问题：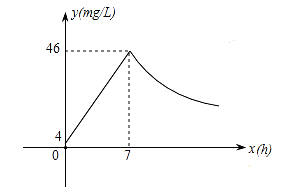
（1）求爆炸前与爆炸后空气中CO浓度y与时间x的函数关系式，并写出相应的自变量取值范围；
（2）矿工只有在空气中的CO浓度降到4 mg/L及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井?
如图，⊙C经过原点且与两坐标轴分别交于A、B两点，点A的坐标为（0，4），M是圆上一点，∠BMO＝120°，求⊙C的半径和圆心C的坐标．
如图，已知反比例函数y1=
的图像与一次函数y2=kx+b的图象交于两点A（-2，1）、B（a，-2）．
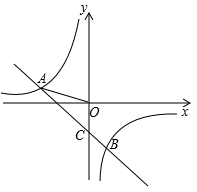
（1）求反比例函数和一次函数的解析式；
（2）若一次函数y2=kx+b的图象交y轴于点C，求△AOC的面积（O为坐标原点）；
（3）求使y1＞y2时x的取值范围．
如图，AB是⊙O的直径，点D在⊙O上，∠DAB＝45°，BC∥AD，CD∥AB
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为1，求图中阴影部分的面积（结果保留π）
某商场开展购物抽奖活动，抽奖箱中有4个标号分别为1，2，3，4的质地、大小相同的小球，顾客任意摸取一个小球，然后放回，再摸取一个小球，若两次摸出的数字之和为“8”是一等奖，数字之和为“6”是二等奖，数字之和为其他数字则是三等奖，请用列举法分别求出顾客抽中一、二、三等奖的概率．
．
的两个实数根．
，且m为整数，求m的值．
，其中
是2x2-2x-7=0的根．
（用配方法解）
粤公网安备 44130202000953号