如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为 ,
,
直线 :
: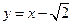 与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与
与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与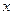
轴相切于点M.
求点A的坐标及∠CAO的度数
⊙B以每秒1个单位长度的速度沿
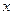 轴向右平移,同时,直线
轴向右平移,同时,直线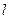 绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线
绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线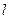 也恰好与⊙B第一次相切,问:直线
也恰好与⊙B第一次相切,问:直线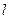 绕点A
绕点A
每秒旋转多少度?如图2,过A、O、C三点作⊙O1,点E为劣弧AO上一点,连接EC、EA、EO,
当点E在劣弧AO上运动时(不与A、O两点重合), 的值是否发生变化?如
的值是否发生变化?如
果不变,求其值;如果变化,说明理由.
右图中,ABCD是梯形,面积是1。已知 =
=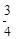 ,
,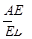 =
= ,
, =
=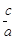 。问:
。问:

(1) 三角形ECD的面积是多少?
(2) 四边形EHFG的面积是多少?
两条并行线上共有k个点,用这k个点恰可以连接1309个三角形,那么k是多少?
如图,设ABCD是正方形,P是CD边的中点,点Q在BC边上,
且ÐAPQ=90°,AQ与BP相交于点T,则 的值为多少?
的值为多少?
已知四边形ABCD中AD//BC,AD:BC=1:2,SDAOF:SDDOE=1:3,SDBEF="24" cm2,求rAOF的面积。
下列m个整数中恰有69个不同的整数,问自然数m的最大值和最小值分别是多少?
[ ],[
],[ ],[
],[ ],…,[
],…,[ ]。
]。
如果一个自然数n能被不超过 的所有的非0自然数整除,我们称自然数n为“牛数”。
的所有的非0自然数整除,我们称自然数n为“牛数”。
请写出所有的牛数。
两条并行线上共有k个点,用这k个点恰可以连接1309个三角形,那么k是多少?
下列m个整数中恰有69个不同的整数,问自然数m的最大值和最小值分别是多少?
[ ],[
],[ ],[
],[ ],…,[
],…,[ ]。
]。
甲、乙、丙三个工程队单独完成某项工程,分别需要140小时、87.5小时、77 时。现在,甲和乙都最多只能工作60小时,丙最多只能工作35小时,三队工作时间之和为100小时完成工程,则甲最多工作多少小时?
时。现在,甲和乙都最多只能工作60小时,丙最多只能工作35小时,三队工作时间之和为100小时完成工程,则甲最多工作多少小时?
如果一个自然数n能被不超过 的所有的非0自然数整除,我们称自然数n为“牛数”。
的所有的非0自然数整除,我们称自然数n为“牛数”。
请写出所有的牛数。
(25分)已知G是△ABC内任一点,BG、CG分别交AC、AB于点E、F.
求使不等式S△BGF·S△CGE≤kS2△ABC恒成立的k的最小值.
已知△ABC中,∠A>∠B>∠C,且∠A=2∠B.若三角形的三边长为整数,面积也为整数,求△ABC面积的最小值.