已知：如图，AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC．求证：DC是⊙O的切线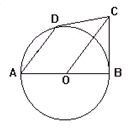
某学校为丰富课间自由活动的内容，随机选取本校100名学生进行调查，调查内容是“你最喜欢的自由活动项目是什么”，整理收集到的数据，绘制成直方图，如图所示．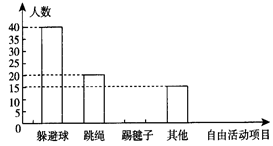
学校采用的调查方式是__________．
求喜欢“踢毽子”的学生人数，并在图中将“踢毽子”部分的图形补充完整；
该校共有800名学生，请估计喜欢“跳绳”的学生人数
我市一家电子计算器专卖店每只进价13元，售价20元，为了扩大销售，该店现规定，凡是一次买10只以上的，每多买1只，所买的全部计算器每只就降低0.10元，例如，某人买20只计算器，于是每只降价0.10×(20－10)=1(元)，因此，所买的全部20只计算器都按照每只19元计算，但是最低价为每只16元。问一次卖多少只获得的利润为120元？
如图∠AOC为直角，OC是∠BOD的平分线，且∠AOB＝28º，求∠BOD的度数。
如图点C在线段AB上，AC＝2BC，M、N分别为AC、BC的中点，若BC＝4cm，求线段MN的长。
如右图,将一张正方形纸片剪成四个形状大小一样的小正方形(称为剪一次), 然后将其中一个小正方形再按相同的方法剪成四个小正形,再将其中一个小正方形剪成四个小正方形,如反复做下去.
填表:
| 剪的次数 |
1 |
2 |
3 |
4 |
5 |
| 小正方形个数 |
|
|
|
|
|
若剪了2011次,共剪出多少个小正方形?
若从矩形一边上的点到对边的视角是直角，即称该点是直角点。例如，如图的矩形
中，点
在
边上，连接
，
,则点为直角点。若点
分别为矩形的边
上的直角点，且
,
,则
的长为 
已知△ABC，∠ACB=90º，AC=BC，点E、F在AB上，∠ECF=45º，设△ABC的面积为S，说明AF·BE=2S的理由。
在萧山区第二届汽车展期间，某汽车经销商推出
四种型号的小轿车共1000辆进行展销．
型号轿车销售的成交率为50%，其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中．参加展销的
型号轿车有多少辆？请你将图2的统计图补充完整；
通过计算说明，哪一种型号的轿车销售情况最好？
问题背景：在
中，
、
、
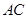三边的长分别为
、
、
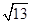，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点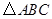（即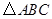三个顶点都在小正方形的顶点处），如图
所示．这样不需求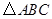的高，而借用网格就能计算出它的面积．请你将
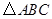的面积直接填写在横线上．__________________
思维拓展：我们把上述求
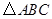面积的方法叫做构图法．若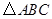三边的长分别为
、
、
（
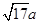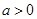），请利用图
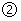的正方形网格（每个小正方形的边长为
）画出相应的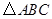，并求出它的面积．
探索创新：若
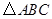三边的长分别为
、
、
（
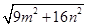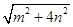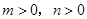，且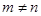
），试运用构图法求出这三角形的面积．
某校学生会准备调查2011级初三同学每天(除课间操外)的课外锻炼时间． 确定调查方式时，甲同学说：“我到（1）班去调查全体同学”；乙同学说：“我到体育场上去询问参加锻炼的同学”；丙同学说：“我到2011级初三每个班去随机调查一定数量的同学”.请你指出哪位同学的调查方式最为合理；
他们采用了最为合理的调查方法收集数据，并绘制出如图1所示的条形统计图和如图2所示的扇形统计图，请将条形统计图补充完整，并在扇形统计图中涂出一块表示“基本不参加”的部分；
若该校2011级初三共有420名同学，请你估计其中每天(除课间操外)课外锻炼时间不超过20分钟的人数．(注：图2中相邻两虚线形成的圆心角均为30°)
春兰集团对应聘者甲、乙、丙进行面试，并从专业知识、工作经验、仪表形象三方面给应聘者打分，每一方面满分20分，最后的打分制成条形统计图(如图)．
填空：根据图中提供的信息，在专业知识方面3人得分的平均数是_____；在工作经验方面3人得分的众数是_____；在仪表形象方面最有优势的是_____。
如果专业知识、工作经验、仪表形象三个方面的重要性之比为10∶7∶3，那么作为人事主管，你应该录用哪一位应聘者?为什么?
上海股民杨百万上星期五交易结束时买进某公司股票1000股，每股50 元，下表为本周内每日该股的涨跌情况 (星期六、日股市休市) (单位：元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+4 |
+4.5 |
-1 |
2.5 |
-5 |
星期三收盘时，每股是多少元
本周内每股最高价多少元？最低价是多少元？
已知买进股票还要付成交金额2‰ 的手续费，卖出时还需付成交额2‰ 的手续费和1‰交易税，如果在星期五收盘前将全部股票卖出，他的收益情况如何？（注意：‰不是百分号，是千分号）
,求
的值
粤公网安备 44130202000953号