如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.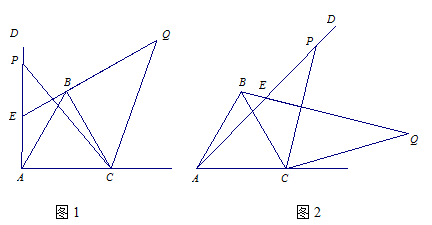
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.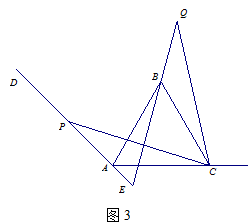
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图(1)中画出四边形OABC;
(3)如图(2),一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
如图所示,菱形ABCD的对角线的长为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于点E,PF∥CD交AD于点F,求阴影部分的面积.
如图,在直角梯形ABCD中,AD∥BC,AD⊥DC,点A关于对角线BD的对称点F刚好落在腰DC上,连接AF交BD于点E,AF的延长线与BC的延长线交于点G,M,N分别是BG,DF的中点.
(1)求证:四边形EMCN是矩形;
(2)若AD=2, ,求矩形EMCN的长和宽.
,求矩形EMCN的长和宽.
如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
已知:如图,在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上,AE=2.
(1)如图(1),当四边形EFGH为正方形时,求△GFC的面积.
(2)如图(2),当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用含a的代数式表示).
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
(1)求∠ABC的度数.
(2)求对角线AC的长度.
(3)求菱形ABCD的面积.
如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1)求∠ABD的度数;
(2)求线段BE的长.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积.