如图,平行四边形 的对角线 、 相交于点 ,点 为 的中点,连接 并延长,交 的延长线于点 ,交 于点 ,连接 、 ,若平行四边形 的面积为48,则 的面积为

| A. |
5.5 |
B. |
5 |
C. |
4 |
D. |
3 |
如图,点 为正六边形 对角线 上一点, , ,则 的值是

| A. |
20 |
B. |
30 |
| C. |
40 |
D. |
随点 位置而变化 |
如图1, 中, , 为锐角.要在对角线 上找点 , ,使四边形 为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案

| A. |
甲、乙、丙都是 |
B. |
只有甲、乙才是 |
| C. |
只有甲、丙才是 |
D. |
只有乙、丙才是 |
如图,在 中, , , , 为 边上的一个动点,连接 , 为 上的一个动点,连接 , ,当 时,线段 的最小值是

| A. |
3 |
B. |
4 |
C. |
5 |
D. |
6 |
如图,在正方形 中, , 是对角线 上的两点,且 ,连接 并延长交 于点 ,连接 并延长交 于点 ,连接 ,则
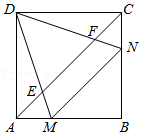
| A. |
|
B. |
|
C. |
1 |
D. |
|
设 为坐标原点,点 、 为抛物线 上的两个动点,且 .连接点 、 ,过 作 于点 ,则点 到 轴距离的最大值
| A. |
|
B. |
|
C. |
|
D. |
1 |
如图1,在矩形 中, 为 边上一点 , .将 沿 翻折得到△ , 的延长线交边 于点 ,过点 作 交 于点 .
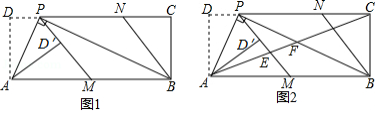
(1)求证: ;
(2)请判断四边形 的形状,并说明理由;
(3)如图2,连接 ,分别交 , 于点 , .若 ,求 的值.
这是一根起点为0的数轴,现有同学将它弯折,如图所示,例如:虚线上第一行0,第二行6,第三行21,…,第10行的数是()
| A.351 | B.702 | C.378 | D.756 |
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的个数是()
①abc>0;②3a+b>0;③﹣1<k<0;④k>a+b;⑤ac+k>0.
A.1 B.2 C.3 D.4
如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于()
A. B.
B. C.3 D.4
C.3 D.4
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()
AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()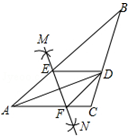
A.2 B.4 C.6 D.8
如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交AB于点F,AF=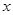
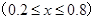 ,EC=
,EC= .则在下面函数图象中,大致能反应
.则在下面函数图象中,大致能反应 与
与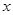 之间函数关系的是
之间函数关系的是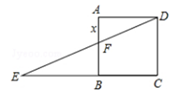

已知反比例函数y= (k>0)的图象与一次函数y=-x+6相交与第一象限的A、B两点,如图所示,过A、B两点分别做x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②△OAM∽△OBN;③若△ABP的面积是8,则k=5;④P点一定在直线y=x上,其中正确命题的个数是()个.
(k>0)的图象与一次函数y=-x+6相交与第一象限的A、B两点,如图所示,过A、B两点分别做x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②△OAM∽△OBN;③若△ABP的面积是8,则k=5;④P点一定在直线y=x上,其中正确命题的个数是()个.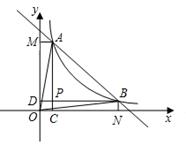
A.1B.2C.3 D.4