初中数学四种命题及其关系选择题

二次函数的图像如图所示，反比列函数与正比列函数在同一坐标系内的大致图像是

某人驾车从A地上高速公路前往B地，中途在服务区休息了一段时间．出发时油箱中存油40升，到B地后发现油箱中还剩油4升，则从出发后到B地油箱中所剩油y（升）与时间t（小时）之间函数的大致图象是（　　）

A．	B．
C．	D．

函数的图象如图所示，下列对该函数性质的论述正确的是

A．该函数的图象是轴对称图形

B．在每个象限内，的值随值的增大而减小

C．当时，该函数在时取得最小值2

D．的值可能为1

小华同学利用假期时间乘坐一大巴车去看望在外打工的妈妈。出发时，大巴的油箱装满油，匀速行驶一段时间后，油箱内的汽油恰剩一半时又加满了油，接着按原速度行驶，到目的地时油箱中还剩有箱汽油。设油箱中所剩汽油量为(升)，时间为（分钟），则与的大致图象是（   ）

如图，正△ABC的边长为3cm,动点P从点A出发，以每秒1cm的速度，沿的方向运动，到达点C时停止，设运动时间为x（秒），,则y关于x的函数的图像大致为【   】
 

A．

B．

C．

D．

小英早上从家里骑车上学，途中想到社会实践调查资料忘带了，立刻原路返回，返家途中遇到给她送资料的妈妈，接过资料后，小英加速向学校赶去．能反映她离家距离s与骑车时间t的函数关系图象大致是

如图，在中，∠C=90°，AB=5cm，BC=3cm，动点P从点A 出发，以每秒1cm的速度，沿ABC的方向运动，到达点C时停止.设,运动时间为t秒，则能反映y与t之间函数关系的大致图象是 （   ）

如图，在△ABC中，∠C=90°，M是AB的中点，动点P从点A出发，
沿AC方向匀速运动到终点C,动点Q从点C出发，沿CB方向匀速运动到终点B.已知P，Q两点同时出发，并同时到达终点.连结MP，MQ，PQ.在整个运动过程中，△MPQ的面积大小变化情况是【   】

A.一直增大      B.一直减小        C.先减小后增大        D.先增大后减小

如下图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度大小不变，则以点A为圆心，线段AP长为半径的圆的面积S与点P的运动时间t之间的函数图像大致为 （      ）

如图，正方形ABCD的边长为a，动点P从点A出发，沿折线A→B→D→C→A的路径运动，回到点A时运动停止．设点P运动的路程长为长为x，AP长为y，则y关于x的函数图象大致是【   】

小明骑自行车上学，开始以正常速度匀速行驶，但行至中途时，自行车出了故障，只好停下来修车，车修好后，因怕耽误上课，他比修车前加快了速度继续匀速行驶，下面是行驶路程s（m）关于时间t（min）的函数图象，那么符合小明行驶情况的大致图象是【   】

若m、n（m<n）是关于x的方程的两根，且a < b，则a、b、m、n 的大小关系是（　 　）

A．m < a < b< n	B．a < m < n < b
C．a < m < b< n	D．m < a < n < b

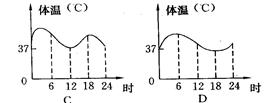
一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了, 中午时亮亮的体温基本正常,但是下午他的体温又开始上升，直到半夜亮亮才感觉身上不那么烫了. 图中能基本上反映出亮亮这一天(0时～24时)体温的变化情况的是(    )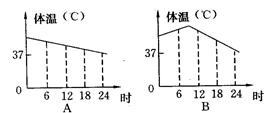

小翔在如图1所示的场地上匀速跑步，他从点A出发，沿箭头所示方向经过点B跑到点C，共用时30秒．他的教练选择了一个固定的位置观察小翔的跑步过程．设小翔跑步的时间为t（单位：秒），他与教练的距离为y（单位：米），表示y与t的函数关系的图象大致如图2所示，则这个固定位置可能是图1中的【   】

A．点M

B．点N

C．点P

D．点Q

如图，为圆O的四等分点，动点从圆心出发，沿路线作匀速运动，设运动时间为（t）．，则下列图象中表示与t之间函数关系最恰当的是（     ）