初中数学圆幂定理试题

如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA为半径的⊙O经过点D。

（1）求证：BC是⊙O切线；
（2）若BD=5， DC=3，求AC的长。

已知：如图，C，D是以AB为直径的⊙O上的两点，且OD∥BC．求证：AD=DC。

正六边形的边长为10 cm，它的边心距等于cm。

下列说法正确的是

A．三点确定一个圆

B．平分弦的直径垂直于弦，并且平分弦所对的两条弧

C．与直径垂直的直线是圆的切线

D．能够互相重合的弧是等弧

如图，∠A是⊙O的圆周角，∠A=50°，则∠BOC的度数为

A．40°

B．50°

C．90°

D．100°

如图，AB是⊙O的直径，C是⊙O上的一点，过点A作AD⊥CD于点D，交⊙O于点E，BC =CE.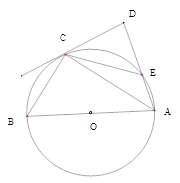

（1）求证：CD是⊙O的切线；
（2）若 tan,BC=3,求DE的长。

已知：如图△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于E，交BC的延长线于点F．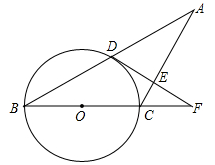

求证：（1）AD=BD；
（2）DF是⊙O的切线．

如图，点A、B、C、D在⊙O上，O在∠D的内部，四边形OABC为平行四边形，则∠OAD＋∠OCD＝         ．

已知圆锥的侧面展开图的圆心角为120°，则这个圆锥的侧面积是底面积的 ．

如图，在△ABC中，AB＝6，AC＝8，BC＝10，D，E分别是AC，AB的中点，则以DE为直径的圆与BC的位置关系是（ ）

A．相交

B．相切

C．相离

D．无法确定

如图，以△ABC的边BC为直径的圆O分别交AB、AC于点D、E，连接OD、OE，若∠A=65°，则∠DOE=（   ）

A．65°         B．50°         C．25°               D．55°

如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F．

（1）求证：DF⊥AC；
（2）若⊙O的半径为8，∠CDF=22．5°，求阴影部分的面积．

边长为2的正六边形的边心距是

A．1

B．2

C．

D．

如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°，则∠BCD的度数为

A．50°

B．80°

C．100°

D．130°

如图，在平面直角坐标系中，直线l的表达式是y=-x+1，长度为2的线段AB在y轴上移动，设点A的坐标为（0，a）．

（1）当以A为圆心，AB为半径的圆与直线l相切时，求a的值；
（2）直线l上若存在点C，使得△ABC是以AB为腰的等腰三角形，则a的取值范围为        ；
（3）直线l上是否存在点C，使得∠ACB=90°？若存在，求出a的取值范围；若不存在，请说明理由．