初中数学圆幂定理计算题

如图， OA=OB，AB交⊙O于点C、D，AC与BD是否相等？为什么？

在△ABC中，P是BC边上的一个动点，以AP为直径的⊙O分别交AB、AC于点E和点F．

（1）若∠BAC＝45°，EF＝4，则AP的长为多少？
（2）在（1）条件下，求阴影部分面积．
（3）试探究：当点P在何处时，EF最短？请直接写出你所发现的结论，不必证明．

如图，AB是⊙O的直径，C是⊙O上一点，AC平分∠BAD；AD⊥ CD，垂足为D．
(1)求证：CD是⊙O的切线
(2)若⊙O的直径为5，CD＝2．求AC的长．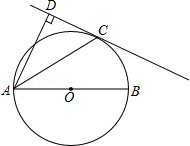

如图，I是△ABC的内心，∠BAC的平分线与△ABC的外接圆相交于点D。BD与ID相等吗？为什么？（12）

尺规作图（保留作图痕迹，不写作法）
某地要修建一处公共服务设施，使它到三所公寓A、B、C 的距离相等．

（1）若三所公寓A、B、C的位置如图所示，请你在图中确定这处公共服务设施（用点P表示）的位置；
（2）若∠BAC＝66º，则∠BPC＝            º.

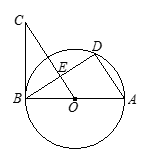
已知：如图，AB为⊙O的直径，AD为弦，∠DBC =∠A.
求证：BC是⊙O的切线；
若OC∥AD，OC交BD于E，BD=6，CE=4，求AD的长.

圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。

如图，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D.已知：AB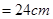, CD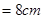

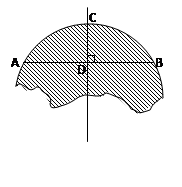
求作此残片所在的圆（不写作法，保留作图痕迹）
求（1）中所作圆的半径

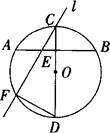
已知：如图，AB是⊙O的一条弦，点C为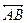的中点，CD是⊙O的直径，过C点的直线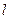交AB所在直线于点E，交⊙O于点F。
（1）判定图中与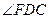的数量关系，并写出结论；
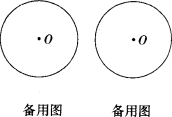
（2）将直线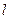绕C点旋转（与CD不重合），在旋转过程中，E点、F点的位置也随之变化，请你在下面两个备用图中分别画出在不同位置时，使（1）的结论仍然成立的图形，标上相应字母，选其中一个图形给予证明。
         

　又PE⊥CB于E，若BC=10，且CE∶EB=3∶2，求AB的长．