初中数学圆幂定理选择题

正八边形的每个内角为（　　）

A．120º

B．135º

C．140º

D．144º

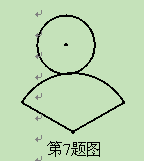
露露从纸上剪下一个圆形和一个扇形纸片（如图），用它们恰好能围成一个圆锥模型。若圆的半径为1，扇形的圆心角等于 $120°$，则此扇形的半径为

A．

$\sqrt{3}$

B．

$\sqrt{6}$

C．

3

D．

6

若⊙O₁、⊙O₂的半径分别为4和6，圆心距O₁O₂=8，则⊙O₁与⊙O₂的位置关系是

A．内切

B．相交

C．外切

D．外离

已知相交两圆的半径分别为4和7，则它们的圆心距可能是（　　）

A．2

B．3

C．6

D．11

在正五边形ABCDE中，对角线AD，AC与EB分别相交于点M，N．下列结论错误的是

A．四边形EDCN是菱形	B．四边形MNCD是等腰梯形
C．△AEM与△CBN相似	D．△AEN与△EDM全等

（11·珠海）圆心角为60°，且半径为3的扇形的弧长为

如图，，点C在上，且点C不与A、B重合，则的度数为（    ）

A．　　  B．或   　　C．　　   D． 或

如图，⊙O的弦AB＝8，M是AB的中点，且OM＝3，则⊙O的半径等于【   】

A．8

B．4

C．10

D．5

已知⊙O的面积为9πcm²，若点0到直线l的距离为πcm，则直线l与⊙O的位置关系是（　　）

A．相交	B．相切
C．相离	D．无法确定

如图，若AB是⊙0的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD=（　　）

A．116°	B．32°
C．58°	D．64°

如图，半径为10的⊙O中，弦AB的长为16，则这条弦的弦心距为（  ）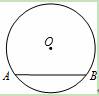

A．6	B．8
C．10	D．12

一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（　　）

A．5π	B．4π
C．3π	D．2π

如图，⊙O的弦AB垂直平分半径OC，若AB=，则⊙O的半径为（　　）

A、          B、
C、           D、

如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（ ▲ )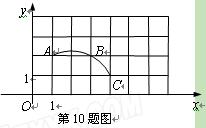

A．点（0，3）	B．点（2，3）
C．点（5，1）	D．点（6，1）

下列命题是真命题的有
①垂直于半径的直线是圆的切线       ②平分弦的直径垂直于弦
③若是方程x－ay=3的解，则a=－1
④若反比例函数的图像上有两点(，y₁)(1，y₂)，则y₁ <y₂

A．1个

B．2个

C．3个

D．4个