2011年初中毕业升学考试(广东深圳卷)数学
如果a>b,c<0,那么下列不等式成立的是( ).
| A. a+c>b+c; | B. c-a>c-b; | C. ac>bc; | D. . . |
抛物线y=-(x+2)2-3的顶点坐标是( ).
| A.(2,-3); | B.(-2,3); | C.(2,3); | D.(-2,-3). |
下列命题中,真命题是( ).
| A.周长相等的锐角三角形都全等; | B.周长相等的直角三角形都全等; |
| C.周长相等的钝角三角形都全等; | D.周长相等的等腰直角三角形都全等. |
矩形ABCD中,AB=8,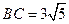 ,点P在边AB上,且BP=3AP,如果圆P是以点P 为圆心,PD为半径的圆,那么下列判断正确的是( ).
,点P在边AB上,且BP=3AP,如果圆P是以点P 为圆心,PD为半径的圆,那么下列判断正确的是( ).
| A.点B、C均在圆P外; | B.点B在圆P 外、点C在圆P内; 外、点C在圆P内; |
| C.点B在圆P内、点C在圆P外; | D.点B、C均在圆P内. |
.有8只型号相同的杯子,其中一等品5只,二等品2只和三等品1只,从中随机抽取1只杯子,恰好是一等品的概率是__________.
某小区2010年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是_________.
如图2,点B、C、D在同一条直线上,CE//AB,∠ACB=90°,如果∠ECD=36°,那么∠A=_________.
如图3,AB、AC都是圆O的弦,OM⊥AB,ON⊥A C,垂足分别为M、N,如果MN=3,那么BC=_________.
C,垂足分别为M、N,如果MN=3,那么BC=_________.
.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________.
(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)如图5,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若 ,求弦MN的长.
,求弦MN的长.
(本题满分10分,第(1)、(2)小题满分各2分,第(3)、(4)小题满分各3分)据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图6)、扇形图(图7).
(1)图7中所缺少的百分数是____________;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是________________(填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是_____________;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有_______________名.

(本题满分12分,每小题满分各6分)如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.联结BF、CD、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如 果DE2=BE·CE,求证四边形ABFC是矩形.
果DE2=BE·CE,求证四边形ABFC是矩形.
(本题满分12分,每小题满分各4分)已知平面直角坐标系xOy(如图1),一次函数 的图像与y轴交于点A,点M在正比例函数
的图像与y轴交于点A,点M在正比例函数 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
(1)求线段AM的长;
(2)求这个二次函数的解析式;
(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图像上,点D在一次函数 的图像上,且四边形ABCD是菱形,求点C的坐标.
的图像上,且四边形ABCD是菱形,求点C的坐标.
今年我市参加中考的毕业生学业考试的总人数约为56000人,这个数据用科学计数法表示为
| A.5.6×103 | B.5.6×104 | C.5.6×105 | D.0.56×105 |
某校开展为“希望小学”捐书活动,以下是八名学生的捐书册数
2 3 2 2 6 7 5 5,这组数据的中位数是
| A.4 | B.4.5 | C.3 | D.2 |
一件服装标价200元,若以六折销售,仍可获利20℅,则这件服装进价是
| A.100元 | B.105元 | C.108元 | D.118元 |
如图3是两个可以自由转动的转盘,转盘各被等分成三个扇形,分别标上1、2、3和6、7、8这6个数字,如果同时转动这两个转盘各一次(指针落在等分线上重转),转盘停止后,指针指向字数之和为偶数的是
A. |
B. |
C. |
D. |

下列命题是真命题的有
①垂直于半径的直线是圆的切线 ②平分弦的直径垂直于弦
③若 是方程x-ay=3的解,则a=-1
是方程x-ay=3的解,则a=-1
④若反比例函数 的图像上有两点(
的图像上有两点( ,y1)(1,y2),则y1 <y2
,y1)(1,y2),则y1 <y2
| A.1个 | B.2个 | C.3个 | D.4个 |
如图4,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为
A.  :1 B.
:1 B. 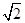 :1 C.5:3 D.不确定
:1 C.5:3 D.不确定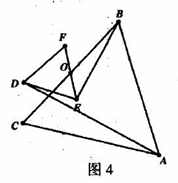
如图7,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为 ,则tanA的值是 .
,则tanA的值是 .
某校为了解本校八年级学生的课外阅读喜好,随即抽取部分该校八年级学生进行问卷调查(每人只选一种书籍),图8是整理数据后画的两幅不完整的统计题,请你根据图中的信息,解答下列问题
(1)这次活动一共调查了 名学生.
(2)在扇形统计图中,“其它”所在的扇形圆心角为 度.
(3)补全条形统计图
(4)若该校八年级有600人,请你估计喜欢“科普常识”的学生有 人.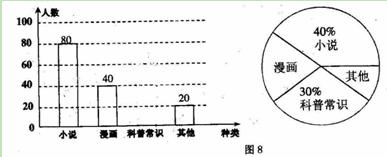
如图9,在⊙O中,点C为劣弧AB的中点,连接AC并延长至D,使CA=CD,连接DB并延长交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图10,连接CE,⊙O的半径为5,AC长为4,求阴影部分面积之和.(保留∏与根号)
如图11,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.
(1)求证:AG=C′G;
(2)如图12,再折叠一次,使点D与点A重合,的折痕EN,EN角AD于M,求EM的长.
深圳某科技公司在甲地、乙地分别生产了17台、15台相同型号的检测设备,全部运往大运赛场A、B两馆,其中运往A馆18台,运往B馆14台,运往A、B两馆运费如表1:
(1)设甲地运往A馆的设备有x台,请填写表2,并求出总运费y(元)与x(台)的函数关系式;
(2)要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案;
(3)当x为多少时,总运费最少,最少为多少元?
如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.
 ;
; ;
; ;
; .
. __________.
__________. _______________.
_______________. (m为常数)有两个相等实数根,那么m=______.
(m为常数)有两个相等实数根,那么m=______.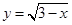 的定义域是_____________.
的定义域是_____________. (k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.
(k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.  ,
, ,那么向量
,那么向量 ____________(结果用
____________(结果用 、
、 表示).
表示).
 +|1-
+|1- |+
|+ .
.
 的相反数是
的相反数是











 cm,则OA= cm.
cm,则OA= cm.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号