初中数学圆幂定理试题

如图，A、B、C为⊙O上三点，∠ACB＝20^○，则∠BAO的度数为    ；

如图，把一个半径为12cm的圆形硬纸片等分成三个扇形，用其中一个扇形制作
成一个圆锥形纸筒的侧面（衔接处无缝隙且不重叠），则圆锥底面半径是   cm．

如图四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠BCD=130º,则∠ADP=              .

在半径为4的⊙O中，点C是以AB为直径的半圆的中点，OD⊥AC，垂足为D，点E是射线AB上的任意一点，DF//AB，DF与CE相交于点F，设EF=，DF=．
(1) 如图1，当点E在射线OB上时，求关于的函数解析式，并写出自变量的取值范围；

(2) 如图2，当点F在⊙O上时，求线段DF的长；
   
(3) 如果以点E为圆心、EF为半径的圆与⊙O相切，求线段DF的长．

如图，在中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA，CB分别相交于点P，Q，则线段PQ长度的最小值是        

如下图，直径为1个单位长度的圆从原点沿数轴向右滚动一周（不滑动），圆上
的一点由原点到达点O′，点O′的坐标是          

如图，AB为⊙O的直径，AC为⊙O的弦，AD平分∠BAC，交⊙O于点D，DE⊥AC，交AC的延长线于点E．

（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若AE＝8，⊙O的半径为5，求DE的长．

如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB=20，分别以DM、CM为直径作两个大小不同和⊙O₁和⊙O₂，则图中所示阴影部分的面积为          .（结果保留）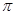

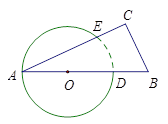
如图，将一个三角形纸板ABＣ的顶点Ａ放在⊙O上，ＡＢ经过圆心．∠Ａ=25°，半径OA=２，则在⊙O上被这个三角形纸板遮挡住的弧的长为　　　　　　　．（结果保留）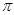
 

如图，已知射线DE与x轴和y轴分别交于点D（3，0）和点E（0，4）．动点C从点M（5，0）出发，以1个单位长度/秒的速度沿x轴向左作匀速运动，与此同时，动点P从点D出发，也以1个单位长度/秒的速度沿射线DE的方向作匀速运动，设运动时间为t秒，

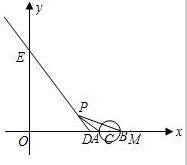
（1）请用含t的代数式分别表示出点C与点P的坐标；
（2）以点C为中心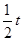，个单位长度为半径的⊙C与x轴交于A、B两点（点A在点B的左侧），连接PA、PB．
①当⊙C与射线DE有公共点时，求t的取值范围；
②当△PAB为等腰三角形时，求t的值．

定义：对于任意的三角形，设其三个内角的度数分别为x°、y°和z°，若满足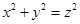，则称这个三角形为勾股三角形．
（1）已知某一勾股三角形的三个内角度数从小到大依次为x°、y°和z°，且xy=2160，求x+y的值；
（2）如图，△ABC是⊙O的内接三角形，AB=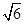，AC=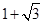，BC=2，BE是⊙O的直径，交AC于D．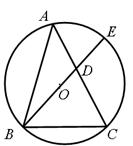         
 
①求证：△ABC是勾股三角形；
②求DE的长．

已知⊙的半径为1，以为原点，建立如图所示的直角坐标系．有一个正方形，顶点的坐标为（，0），顶点在轴上方，顶点在⊙上运动．

（1）当点运动到与点、在一条直线上时，与⊙相切吗？如果相切，请说明理由，并求出所在直线对应的函数表达式；如果不相切，也请说明理由；
（2）设点的横坐标为，正方形的面积为，求出与的函数关系式，并求出的最大值和最小值．

以原点O为圆心，1cm为半径的圆分别交、轴的正半轴于A、B两点，点P的坐标为（2，0），动点Q从点B处出发，沿圆周按顺时针方向匀速运动一周，设运动的时间为秒.

（1）如图一，当时，直线PQ恰好与⊙O第一次相切，连接OQ．求此时点Q的运动速度（结果保留）；
（2）若点Q按照（1）中的速度继续运动.
①当为何值时，以O、P、Q为顶点的三角形是直角三角形；
②在①的条件下，如果直线PQ与⊙O相交，请求出直线PQ被⊙O所截的弦长.

已知：如图，点P是正方形ABCD内的一点，连结PA，PB，PC．

（1）如图甲，将△PAB绕点B顺时针旋转90°到△的位置．
①设AB的长为a，PB的长为b(b<a)，求△PAB旋转到△的过程中边PA所扫过区域 （图甲中阴影部分）的面积；
②若PA＝3，PB＝6，∠APB＝135°，求PC的长．
（2）如图乙，若PA²＋PC²＝2PB²，请说明点P必在对角线AC上．

如图，Rt△ABC中∠C=90°，∠A=30°在AC边上取点O画圆使⊙O经过A、B两点，下列结论中：①；②；③以O为圆心，以OC为半径的圆与AB相切；④延长BC交⊙O与D，则A、B、D是⊙O的三等分点．正确的序号是        ．