[浙江]2012-2013学年浙江温州市育英学校八年级第二学期开学考试数学试卷
两个正数的平均数为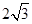 ,其乘积的算术平方根为
,其乘积的算术平方根为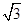 .则其中的大数比小数大( ).
.则其中的大数比小数大( ).
| A.4 | B.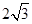 |
C.6 | D.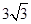 |
如图,在四边形ABCD中,M、N分别是CD、BC的中点, 且AM⊥CD,AN⊥BC,已知∠MAN=74°,∠DBC=41°,则∠ADC度数为( ) .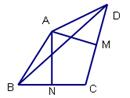
A、45° B、47° C、49° D、51°
反比例函数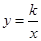 (k>0)与一次函数
(k>0)与一次函数 (b>0)的图像相交于两点
(b>0)的图像相交于两点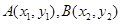 ,线段AB交y轴于点C,当
,线段AB交y轴于点C,当 且AC=2BC时,k、b的值分别为( ).
且AC=2BC时,k、b的值分别为( ).
A.k=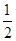 ,b=2 ,b=2 |
B.k=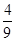 ,b=1 ,b=1 |
C.k=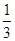 ,b= ,b=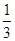 |
D.k=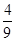 ,b= ,b=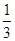 |
已知a、b、2分别为三角形三边,且a、b为方程(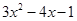 )(
)(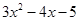 )=12的根,则三角形周长只可能为( ).
)=12的根,则三角形周长只可能为( ).
A. |
B.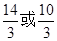 |
C. |
D.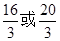 |
在平面直角座标系xoy中,满足不等式x2+y2≤2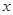 +2y的整数点坐标(x,y)的个数为( ).
+2y的整数点坐标(x,y)的个数为( ).
| A.10 | B.9 | C.7 | D.5 |
在△ABC中,AB=AC=1,BC=x,∠A=36°.则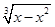 的值为( ).
的值为( ).
A.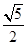 |
B.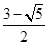 |
C.1 | D. |
已知:二次函数y=x2+bx+c与x轴相交于A(x1,0)、B(x2,0)两点,其顶点坐标为P(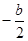 ,
,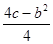 ),AB=|x1-x2|,若S△APB=1,则b与c的关系式是( ).
),AB=|x1-x2|,若S△APB=1,则b与c的关系式是( ).
| A.b2-4c+1=0 | B.b2-4c-1=0 | C.b2-4c+4=0 | D.b2-4c-4=0 |
在边长为2的正方形ABCD的四边上分别取点E、F、G、H、四边形EFGH四边的平方和EF2+FG2+GH2+HE2最小时其面积为 .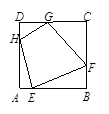
有红、黄、蓝三种颜色的旗帜各三面,在每种颜色的旗帜上分别标有号码1、2、3,现任意抽取3面,它们的颜色与号码均不相同的概率是_________.
如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=_______.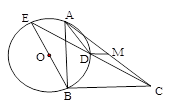
设x1、x2是方程x2-6x+a=0的两个根,以x1、x2为腰和底边的等腰三角形只可以画出一个.试求a的取值范围.
小华早晨6点多钟去学校,去时看了一下手表,发现时针与分针的夹角为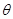 度(0<
度(0<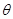 <180,
<180,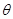 为整数),到了学校,他又看了一下手表,发现此时还不到7点钟,且时针与分针的夹角为也为
为整数),到了学校,他又看了一下手表,发现此时还不到7点钟,且时针与分针的夹角为也为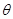 度,若小华去学校途中所用的时间是10的整数倍,那么,小华去学校途中所用的时间是多少?
度,若小华去学校途中所用的时间是10的整数倍,那么,小华去学校途中所用的时间是多少?
已知抛物线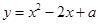 (
(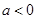 )与
)与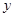 轴相交于点
轴相交于点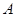 ,顶点为
,顶点为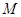 .直线
.直线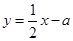 分别与
分别与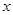 轴,
轴,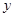 轴相交于
轴相交于 两点,并且与直线
两点,并且与直线 相交于点
相交于点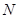 .
.
(1)如图,将 沿
沿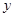 轴翻折,若点
轴翻折,若点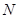 的对应点
的对应点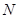 ′恰好落在抛物线上,
′恰好落在抛物线上, ′与
′与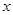 轴交于点
轴交于点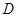 ,连结
,连结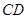 ,求
,求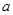 的值和四边形
的值和四边形 的面积;
的面积;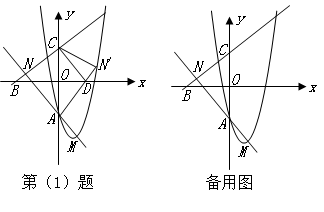
(2)在抛物线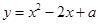 (
(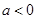 )上是否存在一点
)上是否存在一点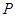 ,使得以
,使得以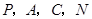 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出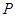 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
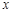 满足
满足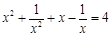 ,则
,则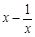 的值是( ).
的值是( ).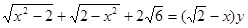 ,则
,则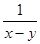 的值为______.
的值为______.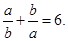
 ________.
________. 满足
满足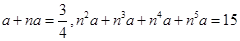 .则
.则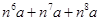 =_________.
=_________.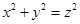 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形.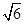 ,AC=
,AC=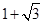 ,BC=2,BE是⊙O的直径,交AC于D.
,BC=2,BE是⊙O的直径,交AC于D. 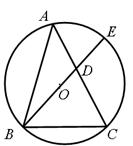
 粤公网安备 44130202000953号
粤公网安备 44130202000953号