初中数学圆幂定理试题

如图，点A、B、C分别是⊙O上的点，CD是⊙O的直径，P是CD延长线上的一点，AP=AC．

（1）若∠ABC=60°．求证：AP是⊙O的切线；
（2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE•AB的值．

如图，⊙O为△ABC的外接圆，BC为⊙O的直径，AE为⊙O的切线，过点B作BD⊥AE于D．

（1）求证：∠DBA=∠ABC；
（2）如果BD=1，tan∠BAD=，求⊙O的半径．

如图，在半径为6cm的⊙O中， A点是劣弧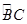的中点，点D是优弧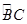上一点，且∠D=30°，下列四个结论：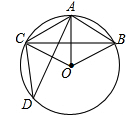

①OA⊥BC；②BC=6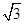m；③sin∠AOB=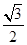；④四边形ABOC是菱形．
其中正确结论的序号是（     ）

A．①③

B．①②③④

C．②③④

D．①③④

如图，已知点D在双曲线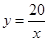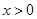（）的图象上，以D为圆心的⊙D与y轴相切于点C（0，4），与x轴交于A，B两点，抛物线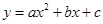经过A，B，C三点，点P是抛物线上的动点，且线段AP与BC所在直线有交点Q．

（1）写出点D的坐标并求出抛物线的解析式；
（2）证明∠ACO=∠OBC；
（3）探究是否存在点P，使点Q为线段AP的四等分点？若存在，求出点P的坐标；若不存在，请说明理由．

如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．

（1）求证：AC是△BDE的外接圆的切线；
（2）若AD=2，AE=6，求EC的长．

如图①、②，在平面直角坐标系中，点A的坐标为（4，0），以点A为圆心，4为半径的圆与轴于O，B两点，OC为弦，∠AOC=60°，P是轴上的一动点，连结CP．

（1）求的度数；
（2）如图①，当与⊙A相切时，求的长；
（3）如图②，当点在直径上时，的延长线与⊙A相交于点，问为何值时，是等腰三角形？

如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．

（1）求证：PA是⊙O的切线；
（2）若，且OC=4，求PA的长和tanD的值．

如图，点在的直径的延长线上，点在上，，

（1）求证：CD是的切线；
（2）若的半径为3，求CD的长．

问题探究：
（一）新知学习：
圆内接四边形的判断定理：如果四边形对角互补，那么这个四边形内接于圆（即如果四边形EFGH的对角互补，那么四边形EFGH的四个顶点E、F、G、H都在同个圆上）．
（二）问题解决：
已知⊙O的半径为2，AB，CD是⊙O的直径．P是上任意一点，过点P分别作AB，CD的垂线，垂足分别为N，M．
（1）若直径AB⊥CD，对于上任意一点P（不与B、C重合）（如图一），证明四边形PMON内接于圆，并求此圆直径的长；
（2）若直径AB⊥CD，在点P（不与B、C重合）从B运动到C的过程汇总，证明MN的长为定值，并求其定值；
（3）若直径AB与CD相交成120°角．
①当点P运动到的中点P₁时（如图二），求MN的长；
②当点P（不与B、C重合）从B运动到C的过程中（如图三），证明MN的长为定值．
（4）试问当直径AB与CD相交成多少度角时，MN的长取最大值，并写出其最大值．

如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．

（1）求证：PA为⊙O的切线；
（2）若OB=5，OP=，求AC的长．

（本题14分）如图，在平面直角坐标系中，O为坐标原点，直线y=－x+4与x轴交于点B，与y轴 交于点A，点C在x轴的负半轴上，并且OC=OB，一动点P在射线AB上运动，连结CP交y轴与点D，连结BD．过B，P，D三点作圆，交y轴与点E，过点E作EF∥x 轴，交圆与点F，连结BF，DF．

（1）求点C的坐标．
（2）若动点P在线段AB上运动，
①求证∠EDB=∠ADP;
②设AP=n，CP=m，求当n为何值时，m的值最小？最小值是多少？
（3）试探究：点P在运动的过程中，当△BDF为直角三角形，并且两条直角边之比为2：1时，请直接写出OD的长              ．

（本题10分）AB，CD是ΘO的两条弦，直线AB，CD互相垂直，垂足为点E，连接AD，过点B作BF⊥AD，垂足为点F，直线BF交直线CD于点G．

（1）如图1，档点E在ΘO外时，连接BC，求证BE平分∠GBC；
（2）如图2，当点E在ΘO内时，连接AC，AG，求证：AC=AG；
（3）如图3，在（2）的条件下，连接BO并延长交AD于点H，若BH平分∠ABF，AG=4，tan∠D=，求线段AH的长．

如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．

（1）若∠E=∠F时，求证：∠ADC=∠ABC；
（2）若∠E=∠F=42°时，求∠A的度数；
（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．

在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB。若PB=4，则PA的长为   ．

如图，是⊙的直径，点是⊙上一点，与过点的切线垂直，垂足为点，直线与的延长线相交于点，弦平分∠，交于点，连接．

（1）求证：平分∠；
（2）求证：PC=PF；
（3）若，AB=14，求线段的长．