初中数学圆幂定理试题

在2015年金华市体育中考中，仰卧起坐就是其中的一项选考项目．图ａ是小明在健身器材上进行仰卧起坐锻炼时情景，图ｂ是小明锻炼时上半身由位置运动到与地面垂直的位置时的示意图．
已知米，米，米．

（1）求的倾斜角的度数（精确到）；
（2）若测得米，试计算小明头顶由点运动到点的路径弧MN的长度（精确到0．01米）．
（参考数据：sin18°≈，cos72°≈，tan17°≈，）

如图2是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图，定长的轮架杆OA，OB，OC抽象为线段，有OA=OB=OC，且∠AOB=120°，折线NG﹣GH﹣HE﹣EF表示楼梯，GH，EF是水平线，NG，HE是铅垂线，半径相等的小轮子⊙A，⊙B与楼梯两边都相切，且AO∥GH．
（1）如图2①，若点H在线段OB时，则的值是______．
（2）如果一级楼梯的高度HE=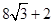cm，点H到线段OB的距离d满足条件d≤3cm，那么小轮子半径r的取值范围是 _______ ．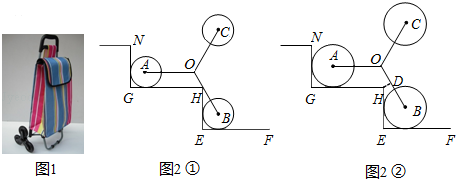

如图，海边有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=96°，为了避免触礁，轮船P与A、B的张角∠APB的最大值为 ．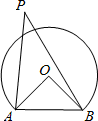

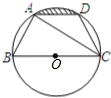
如图，有一圆弧形桥拱，拱形的半径OA=10m，桥拱的跨度AB=16m，则拱高CD= _ __ m．

如图，AB是⊙O的弦，半径OA=20cm，∠AOB=120^o．求：

（1）△OAB的面积．
（2）阴影部分的面积．（精确到1cm²）

⊙O的半径为13，弦AB//CD，AB=24，CD=10，则AB和CD的距离是________．

如图，若BC是⊙O的弦，OD⊥BC于D，且∠BOD=50 ^o，点A在⊙O上（不与B、C重合），则∠BAC=________．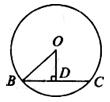

如图，AB是⊙O的直径，C、D在⊙O上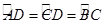，，若∠DAB=58^o，则∠CAB=（）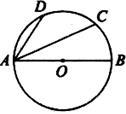

A．20^o B．22^o C．24^o D．26^o

如图，直径CD平分弧AB，请你写出一个正确的结论 ．

如图，AB是半圆O的直径，CD是半圆的三等分点，AB=12，则阴影部分的面积是（）

A．4π

B．6π

C．12π

D．12π-

七年级我们学过三角形的相关知识，在动手实践的过程中，发现了一个基本事实：
三角形的三条高（或三条高所在直线）相交于一点．
其实，有很多八年级、九年级的问题均可用此结论解决．
【运用】如图，已知：△ABC的高AD与高BE相交于点F，且∠ABC=45°，过点F作FG∥BC交AB于点G，求证：FG+CD=BD．

小方同学在解答此题时，利用了上述结论，她的方法如下：
连接CF并延长，交AB于点M，
∵△ABC的高AD与高BE相交于点F，
∴CM为△ABC的高．
（请你在下面的空白处完成小方的证明过程．）
【操作】如图AB是圆的直径，点C在圆内，请仅用无刻度的直尺画出△ABC中AB边上的高．

如图，从圆外一点引圆的两条切线，切点分别为．如果∠APB=60°，PA=8，那么弦AB的长是

已知⊙O的半径为2，直线l上有一点P满足PO=2，则直线l与⊙O的位置关系是（）

A．相切

B．相离

C．相离或相切

D．相切或相交

如图，已知点A、B、C、D均在已知圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10cm．图中阴影部分的面积为 cm²．

如图所示，AB为⊙O的直径，CD为弦，且CD⊥AB，垂足为H．

（1）如果⊙O的半径为4，CD=，求∠BAC的度数；
（2）若点E为的中点，连接OE，CE．求证：CE平分∠OCD；
（3）在（1）的条件下，圆周上到直线AC距离为3的点有多少个？并说明理由．