初中数学圆幂定理试题

如图，A，B，C是⊙O上三点，∠ACB=25°，则∠BAO的度数是（ ）

A．55°

B．60°

C．65°

D．70°

如图，⊙O是△ABC的外接圆，∠OBC=42°，则∠A的度数是（ ）

A．42°

B．48°

C．52°

D．58°

如图，正方形ABCD中，以BC为直径作半圆，BC=2cm．现有两动点E、F，分别从点B、点A同时出发，点E沿线段BA以1cm/秒的速度向点A运动，点F沿折线A-D-C以2cm/秒的速度向点C运动．当点E到达A点时，E、F同时停止运动，设点E运动时间为t．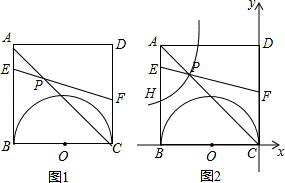

（1）当t为何值时，线段EF与BC平行？
（2）设1＜t＜2，当t为何值时，EF与半圆相切？
（3）如图2，将图形放在直角坐标系中，当1＜t＜2时，设EF与AC相交于点P，双曲线y=（k≠0）经过点P，并且与边AB交于点H，求出双曲线的函数关系式，并直接写出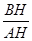的值．

一个圆锥的侧面展开图是半径为18cm，圆心角为的扇形，则这个圆锥的底面半径为       cm．

一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形，边长都为1，则扇形纸板和圆形纸板的面积比是（   ）

A．

B．

C．

D．

如图，以等边三角形ABC的BC边为直径画半圆，分别交AB，AC于点E，D，DF是圆的切线，过点F作BC的垂线交BC于点G．若AF的长为2，则FG的长为（       ）

A．

B．

C．

D．

一个圆锥的母线长是10，高为8，那么这个圆锥的表面积是 （       ）               

A．116π

B．96π

C．80π

D．60π

如图，正方形ABCD的边长等于3，点E是AB延长线上一点，且AE=5，以AE为直径的半圆交BC于点F，则BF=        ．

如图，在矩形ABCD中，AB=3，AD=4，将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′，则点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是          （结果保留π）．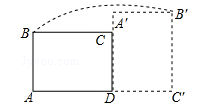

相切两圆的半径分别是5和3，则该两圆的圆心距是     ．

如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆交AB于点D，连接CD，则阴影部分的面积是（ ）

A．

B．

C．

D．

如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC的延长线于点E，与⊙O相交于G、F两点．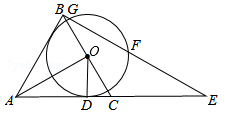

（1）求证：AB与⊙O相切；
（2）若等边三角形ABC的边长是4，求线段BF的长？

如图，在边长为6的正方形ABCD中，E是AB的中点，以E为圆心，ED为半径作半圆，交A、B所在的直线于M、N两点，分别以直径MD、ND为直径作半圆，则阴影部分面积为（ ）

A．       B．      C．       D．

如图，AB是⊙O的直径，C．D是⊙O上的两点，分别连接AC、BC、CD、OD．若∠DOB=140°，则∠ACD=（ ）

A．20°       B．30°       C．40°       D．70°

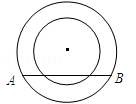
如图，两个同心圆，大圆半径为5cm，小圆的半径为3cm，若大圆的弦AB与小圆相交，则弦AB的取值范围是                 ．