初中数学一次函数的最值填空题

一名考生步行前往考场，5分钟走了总路程的，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1，出租车匀速），则他到达考场所花的时间比一直步行提前了                分钟．

二次函数y＝－x²＋bx＋c的图像如图所示，则一次函数y＝bx＋c的图像不经过第__________象限．

已知一次函数 的图象与 轴正半轴相交，且 随 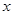的增大而减小，请写出符合上述条件的一个解析式：            ．

如图，是一次函数的图象，当时，y的取值范围是          ．

一次函数的图象过点（0，5），且与正比例函数y=﹣2x的图象平行，则这个一次函数的解析式为  ．

如图，直线y=x+2与抛物线y=ax²+bx+6（a≠0）相交于A（，）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．当△PAC为直角三角形时点P的坐标              ．

已知直线经过点，则关于的不等式的解集是        ．

如图,在平面直角坐标系中,直线L经过原点,且与y轴正半轴所夹的锐角为600,过点A（0,1）作y轴的垂线交直线L于点B,过点B作直线L的垂线交y轴于点A₁,以A₁B、BA为邻边作□ABA₁C₁；过点A₁作y轴的垂线交直线L于点B₁,过点B₁作直线L的垂线交y轴于点A₂,以A₂B₁、B₁A₁为邻边做□A₁B₁A₂C₂,…；按此作法继续下去,则点Cn的坐标是_______．

正方形A₁B₁C₁O，A₂B₂C₂C₁，A₃B₃C₃C₂，…按如图的方式放置，点A₁，A₂，A_3…和点C₁，C₂，C₃…分别在直线y=kx+b（k＞0）和x轴上，已知点B₁（1，1），B₂（3，2），按此规律，则B₄的坐标是                ．

设函数y=x+5与y=的图象的两个交点的横坐标为a、b，则的值是    ．

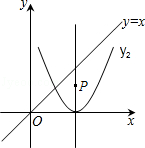
（1）将抛物线y₁=2x²向右平移2个单位，得到抛物线y₂的图象，则y₂=                ；
（2）如图，P是抛物线y₂对称轴上的一个动点，直线x=t平行于y轴，分别与直线y=x、抛物线y₂交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t=                      ．

如图，已知点M的坐标为（3，2），点M关于直线l：y=﹣x+b的对称点落在坐标轴上，则b的值为            ．

如图，直线y=kx+b过A（﹣1，2）、B（﹣2，0）两点，则0≤kx+b≤﹣2x的解集为    ．

已知一次函数y=kx+b的图象如图，则关于x的不等式kx+b﹣1≤0的解集是      ．

已知a、b可以取﹣2、﹣1、1、2中任意一个值（a≠b），则直线y=ax+b的图象不经过第四象限的概率是      ．