初中数学一次函数的最值解答题

如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．
（1）求线段AB所在直线的函数解析式，并写出当0≤y≤2时，自变量x的取值范围；
（2）将线段AB绕点B逆时针旋转90°，得到线段BC，请在答题卡指定位置画出线段BC．若直线BC的函数解析式为y=kx+b，则y随x的增大而　　（填“增大”或“减小”）．

（本小题满分6分）
点A，B，C，D的坐标如图，求直线AB与直线CD的交点坐标

（11·湖州）（本小题10分）
我市水产养殖专业户王大爷承包了30亩水塘，分别养殖甲鱼和桂鱼，有关成本、销售情况如下表：

⑴2010年，王大爷养殖甲鱼20亩，桂鱼10亩，求王大爷这一年共收益多少万元？（收益=销售额－成本）
⑵2011年，王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼，计划投入成本不超过70万元。若每亩养殖的成本、销售额与2010年相同，要获得最大收益，他应养殖甲鱼和桂鱼各多少亩？
⑶已知甲鱼每亩需要饲料500㎏，桂鱼每亩需要饲料700㎏，根据⑵中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍，结果运输养殖所需要全部饲料比原计划减少了2次，求王大爷原定的运输车辆每次可装载饲料多少㎏？

（11·湖州）（本小题6分）
已知：一次函数y=kx＋b的图象经过M（0，2），（1，3）两点。
⑴求k，b的值；
⑵若一次函数y=kx＋b的图象与x轴交点为A（a，0），求a的值。

今年我省干旱灾情严重，甲地急需要抗旱用水15万吨，乙地13万吨．现
有A、B两水库决定各调出14万吨水支援甲、乙两地抗旱．从A地到甲地50千米，到乙
地30千米；从B地到甲地60千米，到乙地45千米．
⑴设从A水库调往甲地的水量为x万吨，完成下表

⑵请设计一个调运方案，使水的调运总量尽可能小．（调运量＝调运水的重量×调运的距离，单位：万吨•千米）

北京时间2011年3月11日46分，日本东部海域发生9级强烈地震并引发海啸．在其灾区，某药品的需求量急增．如图所示，在平常对某种药品的需求量y1（万件）．供应量y2（万件）与价格x（元∕件）分别近似满足下列函数关系式：，，需求量为0时，即停止供应．当时，该药品的价格称为稳定价格，需求量称为稳定需求量．
（1）求该药品的稳定价格与稳定需求量．
（2）价格在什么范围内，该药品的需求量低于供应量？
（3）由于该地区灾情严重，政府部门决定对药品供应方提供价格补贴来提高供货价格，以提高供应量．根据调查统计，需将稳定需求量增加6万件，政府应对每件药品提供多少元补贴，才能使供应量等于需求量．

（11·漳州）（满分13分）如图，直线y＝－2x＋2与x轴、y轴分别交于A、B两点，将△OAB绕点O逆时针方向旋转90°后得到△OCD．

（1）填空：点C的坐标是(_  ▲  ，_  ▲  )，
点D的坐标是(_  ▲  ，_  ▲  )；
（2）设直线CD与AB交于点M，求线段BM的长；
（3）在y轴上是否存在点P，使得△BMP是等腰三角形？若存在，
请求出所有满足条件的点P的坐标；若不存在，请说明理由．

某企业为重庆计算机产业基地提供电脑配件，受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y₁（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：

月份x	1	2	3	4	5	6	7	8	9
价格y1（元/件）	560	580	600	620	640	660	680	700	720

随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格y₂（元）与月份x（10≤x≤12，且x取整数）之间存在如图所示的变化趋势：

（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y₁与x之间的函数关系式，根据如图所示的变化趋势，直接写出y₂与x之间满足的一次函数关系式；
（2）若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p₁（万件）与月份x满足函数关系式p₁=0.1x+1.1（1≤x≤9，且x取整数）10至12月的销售量p₂（万件）与月份x满足函数关系式p₂=﹣0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；
（3）今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少0.1a%．这样，在保证每月上万件配件销量的前提下，完成了1至5月的总利润1700万元的任务，请你参考以下数据，估算出a的整数值．
（参考数据：99²=9901，98²=9604，97²=9409，96²=9216，95²=9025）

小王从A地前往B地，到达后立刻返回，他与A地的距离y（千米）和所用的时间x（小时）之间的函数关系如图所示。
（1）小王从B地返回A地用了多少小时？
（2）求小王出发6小时后距A地多远？
（3）在A、B之间友谊C地，小王从去时途经C地，到返回时路过C地，共用了2小时20分，求A、C两地相距多远？

甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备
后，乙组的工作效率是原来的2倍．两组各自加工零件的数量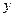(件)与时间(时)的函数图
象如图所示．
（1）求甲组加工零件的数量y与时间之间的函数关系式．
（2）求乙组加工零件总量的值．
（3）甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？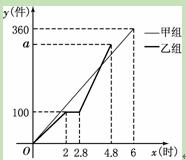

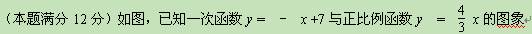
交于点A，且与x轴交于点B.
（1）求点A和点B的坐标；
（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从点O出发，以每秒1个单位长的速度，沿O—C—A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒.
①当t为何值时，以A、P、R为顶点的三角形的面积为8？
②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不存在，请说明理由．

如图1是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形铁块立放其中（圆柱形铁块的下底面完全落在乙槽底面上）．现将甲槽的水匀速注入乙槽，甲、乙两个水槽中水的深度（厘米）与注水时间（分钟）之间的关系如图2所示．根据图象提供的信息，解答下列问题：
（1）图2中折线表示________槽中水的深度与注水时间的关系，线段表示_______槽中水的深度与注水时间之间的关系（以上两空选填“甲”或“乙”），点的纵坐标表示的实际意义是________________________________；
（2）注水多长时间时，甲、乙两个水槽中水的深度相同？
（3）若乙槽底面积为36平方厘米（壁厚不计），求乙槽中铁块的体积；
（4）若乙槽中铁块的体积为112立方厘米，求甲槽底面积（壁厚不计）．（直接写出结果）

因长期干旱，甲水库蓄水量降到了
正常水位的最低值．为灌溉需要，由乙水库向甲水库匀速
供水，20h后，甲水库打开一个排灌闸为农田匀速灌溉，
又经过20h，甲水库打开另一个排灌闸同时灌溉，再经过
40h，乙水库停止供水．甲水库每个排泄闸的灌溉速度相
同，图中的折线表示甲水库蓄水量Q (万m³) 与时间t (h) 之间的函数关系．
求：（1）线段BC的函数表达式；
（2）乙水库供水速度和甲水库一个排灌闸的灌溉速度；
（3）乙水库停止供水后，经过多长时间甲水库蓄水量又降到了正常水位的最低值？

小华观察钟面（图1），了解到钟面上的分针每小时旋转360度，时针毎小时旋转30度．他为了进一步探究钟面上分针与时针的旋转规律，从下午2：00开始对钟面进行了一个小时的观察．为了探究方便，他将分针与分针起始位置OP（图2）的夹角记为y₁，时针与OP的夹角记为y₂度（夹角是指不大于平角的角），旋转时间记为t分钟．观察结束后，他利用获得的数据绘制成图象（图3），并求出y₁与t的函数关系式：
请你完成：
（1）求出图3中y₂与t的函数关系式；
（2）直接写出A、B两点的坐标，并解释这两点的实际意义；
（3）若小华继续观察一个小时，请你在题图3中补全图象．

如图，在平面直角坐标系中，直线分别交轴，轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．
（1）直接写出点A，B的坐标，并求直线AB与CD交点的坐标；
（2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点M从点A出发，沿线段AB以每秒个单位长度的速度向终点B运动，过点P作，垂足为H，连接，．设点P的运动时间为秒．
①若△MPH与矩形AOCD重合部分的面积为1，求的值；
②点Q是点B关于点A的对称点，问是否有最小值，如果有，求出相应的点P的坐标；如果没有，请说明理由．