如图，直线y = kx+6与x轴y轴分别相交于点E，F。点E的坐标为（- 8，0），点A的坐标为（- 6，0）。 点P（x，y）是第二象限内的直线上的一个动点。
（1）求k的值；
（2）当点P运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
（3）探究：当P运动到什么位置（求P的坐标）时，△OPA的面积为
，并说明理由
现正是闽北特产杨梅热销的季节，某水果零售商店分两批次从批发市场共购进杨梅40箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款700元．
（1）设第一、二次购进杨梅的箱数分别为a箱、b箱，求a，b的值；
（2）若商店对这40箱杨梅先按每箱60元销售了x箱，其余的按每箱35元全部售完．
①求商店销售完全部杨梅所获利润y（元）与x（箱）之间的函数关系式；
②当x的值至少为多少时，商店才不会亏本．
（注：按整箱出售，利润=销售总收入﹣进货总成本）
某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：
（1）设商场购进A型节能台灯为x盏，销售完这批台灯时可获利为y元，求y关于x的函数解析式；
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
某工厂生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本
（万元/吨）与产量
（吨）之间是一次函数关系，函数
与自变量的部分对应值如下表：
| （吨） |
10 |
20 |
30 |
| （万元/吨） |
45 |
40 |
35 |
（1）求
与
的函数关系式，并写出自变量的取值范围；
（2）当投入生产这种产品的总成本为1200万元时，求该产品的总产量；（注：总成本=每吨成本×总产量）
（3）市场调查发现，这种产品每月销售量
（吨）与销售单价
（万元/吨）之间满足如图所示的函数关系．该厂第一个月按同一销售单价卖出这种产品25吨，请求出该厂第一个月销售这种产品获得的利润．（注：利润=售价—成本）
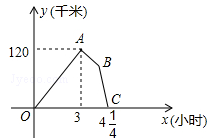
甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．
请结合图象信息解答下列问题：
（1）直接写出a的值，并求甲车的速度；
（2）求图中线段EF所表示的y与x的函数关系式，并直接写出自变量x的取值范围；
（3）乙车出发多少小时与甲车相距15千米？直接写出答案．
某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后缷完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离y（千米）与货车行驶时间x（小时）之间的函数图象如图所示，现有以下4个结论：
①快递车从甲地到乙地的速度为100千米/时；
②甲、乙两地之间的距离为120千米；
③图中点B的坐标为（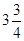
，75）；
④快递车从乙地返回时的速度为90千米/时，以上4个结论正确的是 ．
“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．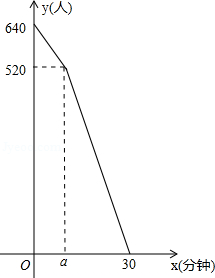
（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？
已知一次函数y=kx+b的图象经过点（﹣1，﹣5），且与正比例函数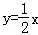
的图象相交于点（2，m）．
求：（1）m的值；
（2）一次函数y=kx+b的解析式；
（3）这两个函数图象与x轴所围成的三角形面积．
“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．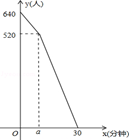
（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？
国庆长假，小明从老家乘车去上海．一路上，小明记下了如下数据（注：“上海90km”表示离上海的距离为90km）：
| 观察时间 |
10：30（t=0） |
10：36（t=6） |
10：30（t=18） |
| 路牌内容 |
上海90Km |
上海80Km |
上海60Km |
假设汽车离上海的距离s（km）是行驶时间t（min）的一次函数，求s关于t的函数关系式．
已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数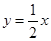
的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．
自2012年6月1日起，全国实施了阶梯电价．某省出台了阶梯电价方案：电价分“三档”收费，第一档为a度，居民用电量低于a度的部分，执行现行的标准电价（0．53元/度）；第二档为a～b度，居民月用电量在a～b之间的部分，电价在一档电价的基础上提高0．05元/度；第三档为超过b度，居民月用电量高于b度的部分，电价在一档电价的基础上提高m元/度．实施阶梯电价后，月电费y（元）与月用电量x（度）之间的函数关系如图所示．
（1）求a，b，m的值；
（2）求y与x之间函数关系式，并写出自变量x的取值范围．
某饮料厂为了开发新产品，用
种果汁原料和
种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制
千克，两种饮料的成本总额为
元．
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与之间的函数关系式．
（2）若用19千克种果汁原料和17．2千克种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；
请你列出关于且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使值最小，最小值是多少？
暑假期间，小明和父母一起开车到距家200千米的景点旅游．出发前，汽车油箱内储油45升；当行驶150千米时，发现油箱剩余油量为30升．
（1）已知油箱内余油量y（升）是行驶路程x（千米）的一次函数，求y与x的函数关系式；
（2）当油箱中余油量少于3升时，汽车将自动报警．如果往返途中不加油，他们能否在汽车报警前回到家？请说明理由．
粤公网安备 44130202000953号