如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
已知直线y=kx+b经过点(0,-2)和点(-2,0).
⑴求直线的解析式;
⑵在图中画出直线,并观察 >1时,
>1时, 的取值范围(直接写答案);
的取值范围(直接写答案);
⑶求此直线与两坐标轴围成三角形的面积;
已知:一次函数 的图象经过M(0,2),(1,3)两点.
的图象经过M(0,2),(1,3)两点.
⑴求k、b的值;
⑵若一次函数 的图象与x轴的交点为A(a,0),求a的值.
的图象与x轴的交点为A(a,0),求a的值.
向长20m、宽10m的长方形游泳池内注水,每小时水位上升0.2m。
⑴如果x h共注水ym3,那么y=
⑵注水时间x(h)与游泳池水深d(m)的函数关系是d=
⑶当水深为1.6m时即可开放使用,此时该游泳池内共注水 M3
如图:正方形OABC中,B点的坐标为(2,2).D、E分别在边AB、BC上,F在BC的延长线上.且AD=CF,∠EDO=∠DOC.
(1)猜想△OAD与△OCF能否通过旋转重合?请证明你的猜想.
(2)若D是AB的中点.求直线DE的解析线.
设一次函数 的图象为
的图象为 ,一次函数
,一次函数 的图象为直线
的图象为直线 ,若
,若 ,且
,且 ,我们就称直线
,我们就称直线 与直线
与直线 互相平行.解答下面的问题:
互相平行.解答下面的问题:
(1)求过点P(1,4)且与已知直线 平行的直线的函数表达式,并画出直
平行的直线的函数表达式,并画出直
线的图象;
(2)设(1)中的直线分别与 轴、y轴交于A、B两点,直线
轴、y轴交于A、B两点,直线 分别与
分别与 轴、
轴、
y轴交于C、D两点,求四边形ABCD的面积.
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计费;月用水量超过20m3时,其中的20m3仍按2元/m3收费,超过部分按2.6元/m3计费.设每户家庭用用水量为xm3时,应交水费y元.
(1)分别求出 和x>20时y与x的函数表达式;
和x>20时y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 |
四月份 |
五月份 |
六月份 |
| 交费金额 |
30元 |
34元 |
42.6元 |
小明家这个季度共用水多少立方米?
如图,一条直线过点A(0,4),B(2,0),将这条直线向左平移与x轴、y轴的负半轴分别交于点C、D,使DB=DC.
(1)求直线CD的函数解析式;
(2)求△BCD的面积;
(3)在直线AB或直线CD上是否存在点P,使△PBC的面积等于△BCD的面积的2倍?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)琚租书时间x(天)之间的关系如下图所示。
(1)分别求出用租书卡和会员卡租书的金额y(元)琚租书时间x(天)之间的关系式;
(2)两种租书方式每天租书的收费分别是多少元(不含卡费)
(3)若两种租书卡使用期限均为一年(一年按365天计算),则这一年中如何选取这两种租书方式比较合算?
已知函数
(1)画出这个函数的图象;
(2)写出这个函数的图象与x轴,y轴的交点坐标
(3)求此函数的图象与坐标轴围成的三角形的面积。
如图,已知直线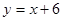 的图象与
的图象与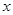 轴、
轴、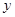 轴交于
轴交于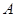 、
、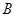 两点。
两点。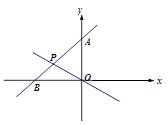
(1)求点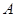 、点
、点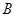 的坐标和△
的坐标和△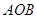 的面积。
的面积。
(2)求线段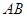 的长。
的长。
(3)若直线l经过原点,与线段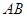 交于点
交于点 (
( 为一动点),把△
为一动点),把△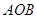 的面积分成2︰1两部分,求直线L的解析式。
的面积分成2︰1两部分,求直线L的解析式。
已知一次函数 。求:
。求:
(1)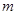 、
、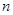 为何值时,函数图象经过原点?
为何值时,函数图象经过原点?
(2)若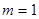 ,
,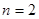 时,求此一次函数的图象与两坐标轴围成的面积。
时,求此一次函数的图象与两坐标轴围成的面积。
小明准备节约一些储存起来,他已存有60元,从2012年元月份起每个月存15元;小亮以前没存钱,听到小明在存零用钱,表示也从2012年元月份起每个月存25元.
(1)试写出小明的存款总数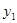 (元)与从2012年元月份起的月数
(元)与从2012年元月份起的月数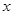 之间的函数关系式以及小亮的存款总数
之间的函数关系式以及小亮的存款总数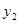 (元)与月数
(元)与月数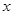 之间的函数关系式.
之间的函数关系式.
(2)从第几个月开始小亮的存款数可以超过小明?
某办公用品销售商店推出两种优惠方式:①购一个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠。书包每个定价20元,水性笔每支定价5元。小丽和同学需要买4个书包,水性笔若干支(不少于4支)。
(1)分别写出两种优惠方式购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)对x的取值情况进行分析,说明按哪种优惠方式购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济。
在平面直角坐标系xoy中,边长为 的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
⑴当∠BAO=45°时,求点P的坐标;
⑵求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上;
⑶当B点坐标为(0,1)时,求CD的解析式。