甲、乙两同学在一次百米赛跑中，路程S（米）与时间t（秒）之间的关系如图所示．根据图象回答下列问题：
（1）3.8秒时，哪位同学处于领先位置？
（2）在这次赛跑中，哪位同学先到达终点？比另一个同学早多少时间到达？约几秒后哪位同学被哪位同学追上？
（3）甲同学所走的路程S（米）与时间t（秒）之间的函数关系式．
如图，直线l的解析式为
，它与坐标轴分别交于A、B两点，其中B坐标为（0，4）．
（1）求出A点的坐标；
（2）若点 P在y轴上，且到直线l的距离为3，试求点P的坐标；
（3）在第一象限的角平分线上是否存在点Q使得∠QBA=90°；若存在，求点Q的坐标，若不存在，请说明理由．
（4）动点C从y轴上的点（0，10）出发，以每秒1cm的速度向负半轴运动，求出点C运动所有的时间t，使得△ABC为轴对称图形．
已知一次函数y=mx+m－2与y=2x－3的图象的交点A在y轴上，它们与x轴的交点分别为点B、点C．
（1）求m的值及△ABC的面积；
（2）求一次函数y=mx+m－2的图像上到x轴的距离等于2的点的坐标．
已知到直线l的距离等于a的所有点的集合是与直线l平行且距离为a的两条直线l1、l2（如图①）．
（1）在图②的平面直角坐标系中，画出到直线y=x＋2
的距离为1的所有点的集合的图形．并写出该图形与y轴交点的坐标．
（2）试探讨在以坐标原点O为圆心，r为半径的圆上，到直线y=x＋2的距离为1的点的个数与r的关系．
（3）如图③，若以坐标原点O为圆心，2为半径的圆上只有两个点到直线y=x＋b的距离为1，则b的取值范围为 ．
某饮料厂为了开发新产品，用
种果汁原料和
种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制
千克，两种饮料的成本总额为
元．
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与之间的函数关系式．
（2）若用19千克种果汁原料和17．2千克种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；
请你列出关于且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使值最小，最小值是多少？
某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：
，且物价部门规定这种绿茶的销售单价不得高于90元/千克．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：
（1）求出y与x之间的函数关系式；
（2）当x取何值时，y的值最大？最大值为多少？
（3）如果公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？
如图：一次函数的图象与反比例函数
的图象交于A（－2，6）和点B（4，n）
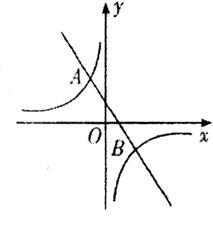
（1）求反比例函数的解析式和B点坐标
（2）根据图象直接回答，在什么范围时，一次函数的值大于反比例函数的值．
如图，一次函数y=－
x+3的图象与x轴和y轴分别交于点A和B ，再将△AOB沿直线CD对折，使点A与点B重合．直线CD与x轴交于点C，与AB交于点D．
（1）点A的坐标为 ，点B的坐标为 。
（2）求OC的长度;
（3）在x轴上有一点P，且△PAB是等腰三角形，不需计算过程，直接写出点P的坐标．
在直角坐标系xOy中，直线l过（1，3）和（2，1）两点，且与x轴，y轴分别交于A，B两点．
（1）求直线l的函数关系式；
（2）求△AOB的面积．
已知一次函数的图象过点（3，5）与（
，
），且该图象与x轴、y轴分别交于点A、点B，点O为坐标原点，
（1）求这个一次函数表达式；
（2）求△OAB的面积．
为了贯彻落实市委市府提出的“精准扶贫”精神．某校特制定了一系列关于帮扶A、B两贫困村的计划．现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如下表：
| 目的地 车型 |
A村（元/辆） |
B村（元/辆） |
| 大货车 |
800 |
900 |
| 小货车 |
400 |
600 |
（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
粤公网安备 44130202000953号
与
的函数关系式； 
时的函数值．