初中数学一次函数的最值试题

如图，一次函数y₁=k₁x+b的图象和反比例函数y₂=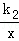的图象交于A（1，2），B（﹣2，﹣1）两点，若y₁＜y₂，则x的取值范围是（　　）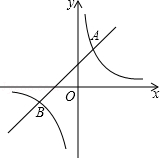

A．x＜1	B．x＜﹣2
C．﹣2＜x＜0或x＞1	D．x＜﹣2或0＜x＜1

某通讯公司推出了①②两种收费方式，收费y₁，y₂ （元）与通讯时间x（分钟）之间的函数关系如图所示，则使不等式kx+30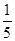＜x成立的x的取 值范围是          ．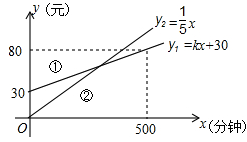

已知直线y=x-a与y=-x+b相交于点（1，0），则不等式x-a≥-x+b的解集是               ．

小刚从家骑车上学，先上坡到达A地后再下坡到达学校，所用的时间与路程如图所示．如果返回时，上、下坡速度依然保持不变，那么小刚从学校回到家需要的时间是_________分钟．

函数y=x-1的图象是（　　）

如图，点P是在□ABCD边上一动点，沿A→D→C→B的路径移动，设P点经过的路径长为x，△BAP的面积是y，则下列能大致反映y与x的函数关系的图象是

某书定价25元，如果一次购买20本以上，超过20本的部分打八折，试写出付款金额y（单位：元）与购书数量x（单位：本）之间的函数关系          ．

将直线y=3x+1平移向下平移4个单位，则平移后的解析式为      ．

过点P（8，2）且与直线y=x+1平行的一次函数解析式为_________．

某气球内充满一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m³）的反比例函数，其图象如图所示．

（1）写出这一函数的表达式．
（2）当气体体积为1 m³时，气压是多少？
（3）当气球内的气压大于140 kPa时，气球将爆炸，为了安全考虑，气体的体积应不小于多少？

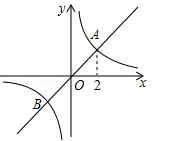
如图，正比例函数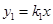的图象与反比例函数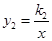的图象相交于A，B两点，其中点A的横坐标为2，当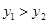时，x的取值范围是（ ）

A．x＜﹣2或x＞2

B．x＜﹣2或0＜x＜2

C．﹣2＜x＜0或0＜x＜﹣2

D．﹣2＜x＜0或x＞2

为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y＝－2x＋80．设这种产品每天的销售利润为w元．
（1）求w与x之间的函数关系式；
（2）该产品销售价定为每千克多少元时，每天的销售利润最大？最大是多少元？
（3）如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？

已知直线l为x+y=8，点P（x，y）在l上，且x＞0，y＞0，点A的坐标为（6，0）．

（1）设△OPA的面积为S，求S与x的函数关系式，并直接写出x的取值范围；
（2）当S=9时，求点P的坐标；
（3）在直线l上有一点M，使OM+MA的和最小，求点M的坐标．

小张的爷爷每天坚持体育锻炼，星期天爷爷从家里跑步到公园，打了一会太极拳，然后沿原路慢步走到家，下面能反映当天爷爷离家的距离y（米）与时间t（分钟）之间关系的大致图象是（ ）

A．

B．

C．

D．

直线y=kx+b不经过第四象限，则（　　）

A．k＞0，b＞0

B．k＜0，b＞0

C．k≥0，b≥0

D．k＜0，b≥0