一个足球从地面上被踢出,它距地面高度y(米)可以用二次函数y=-4.9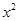 +19.6x刻画,其中x(秒)表示足球被踢出后经过的时间.则足球被踢出后到离开地面达到最高点所用的时间是 秒.
+19.6x刻画,其中x(秒)表示足球被踢出后经过的时间.则足球被踢出后到离开地面达到最高点所用的时间是 秒.
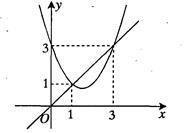
已知二次函数y=ax2+bx+c与一次函数y=x的图象如图所示,给出以上结论:
①b2-4ac>0;
②a+b+c=1;
③当1<x<3时,ax2+(b-1)x+c<0;
④二次函数y=ax2+(b-1)x+c的图象经过点(1,0)和(3,0).
其中正确的有: (把你认为正确结论的序号都填上).
二次函数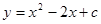 的图象与x轴的一个交点坐标为(3,0),则与y轴的交点坐标为 .
的图象与x轴的一个交点坐标为(3,0),则与y轴的交点坐标为 .
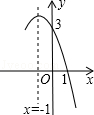
抛物线y=-x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .

对于抛物线y=ax2+bx+c(a≠0),有下列说法:
①当b=a+c时,则抛物线y=ax2+bx+c一定经过一个定点(﹣1,0);
②若△=b2﹣4ac>0,则抛物线y=cx2+bx+a与x轴必有两个不同的交点;
③若b=2a+3c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
④若a>0,b>a+c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
其中正确的有 .
抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .
把抛物线y=﹣x2向上平移2个单位,那么所得抛物线与x轴的两个交点之间的距离是 .
将二次函数 的图象向右平移1个单位,再向下平移4个单位,所得二次函数的解析式为
的图象向右平移1个单位,再向下平移4个单位,所得二次函数的解析式为
已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+b(k≠0)的图象相交于点A(﹣2,4),B(8,2)(如图所示),则能使y1>y2成立的x的取值范围是 .

如图,已知函数y= 与y=ax2+bx(a>0,b>0)的图象交于点P.点P的纵坐标为1.则关于x的方程ax2+bx+
与y=ax2+bx(a>0,b>0)的图象交于点P.点P的纵坐标为1.则关于x的方程ax2+bx+ =0的解为 .
=0的解为 .

已知(-3,m)、(1,m)是抛物线y=2x2+bx+3的两点,则b=______.