在同一平面直角坐标系中,函数y=kx+k和函数y=﹣kx2+4x+4(k是常数,且k≠0)的图象可能是( )
A. |
B. |
C. |
D. |
如图所示,在平面直角坐标中,抛物线的顶点P到x轴的距离是4,抛物线与x轴相交于O、M两点,OM=4;矩形ABCD的边BC在线段的OM上,点A、D在抛物线上.
(1)求这条抛物线的解析式;
(2)设D(m,n),矩形ABCD的周长为l,写出l与m的关系式,并求出l的最大值;
(3)点E在抛物线的对称轴上,在抛物线上是否还存在点F,使得以E、F、O、M为顶点的四边形是平行四边形?如果存在,写出F点的坐标.
(课改)现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x小明掷B立方体朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为( )
A. B.
B. C.
C. D.
D.
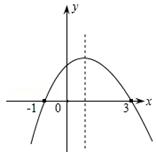
如下左图为二次函数 (a≠0)的图象,则下列说法:
(a≠0)的图象,则下列说法:
①a>0;②2a+b=0;③a+b+c>0;④当﹣1<x<3时,y>0.
其中正确的个数为( )
| A.1 | B.2 | C.3 | D.4 |
如图,在平面直角坐标系xoy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
(1)求抛物线的解析式;
(2)若两动点M、H分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头,并以每秒 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
如图,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,且交y轴于点C,对称轴与抛物线相交于点P、与直线BC相交于点M.
(1)求该抛物线的解析式.
(2)在抛物线上是否存在一点N,使得|MN-ON|的值最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(3)连接PB,请探究:在抛物线上是否存在一点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
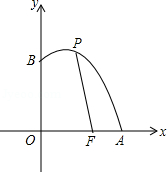
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5﹣ (0≤x≤5),给出以下四个结论:
(0≤x≤5),给出以下四个结论:
①AF=2;②BF=5;③OA=5;④OB=4
其中正确结论的序号是 .
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).
(1)求该抛物线的解析式及顶点M坐标;
(2)求△BCM面积与△ABC面积的比;
(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.
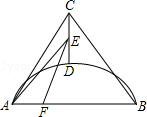
如图,AC=BC,点D是以线段AB为弦的圆弧的中点,AB=4,点E、F分别是线段CD,AB上的动点.设AF=x,AE2﹣FE2=y,则能表示y与x的函数关系的图象是( )
A.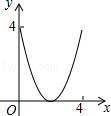 |
B.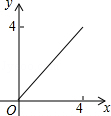 |
C.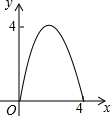 |
D.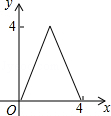 |
在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的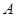 处飞出(
处飞出(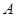 在
在 轴上),运动员孙可在距
轴上),运动员孙可在距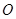 点6米的
点6米的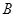 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.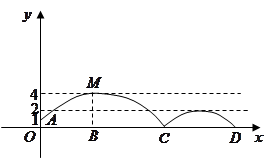
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 距守门员多少米?(取
距守门员多少米?(取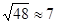 )
)
(3)孙可要抢到足球第二个落地点 ,他应从第一次落地点
,他应从第一次落地点 再向前跑多少米?(取
再向前跑多少米?(取 )
)
已知下列函数:
①y=x2;
②y=-x2;
③y=2x2;
④y=(x-1)2+2.
其中通过平移、旋转、轴对称变换得到函数y=x2+2x-3的图象的有 (填写所有正确选项的序号).
如图,直线 与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线
与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线 与x轴的另一个交点为A,顶点为P.
与x轴的另一个交点为A,顶点为P.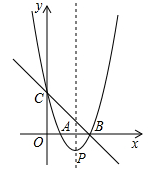
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
将抛物线 的图象向右平移3个单位,再向上平移4个单位后,得到的新抛物线解析式是 .
的图象向右平移3个单位,再向上平移4个单位后,得到的新抛物线解析式是 .