初中数学一元二次方程的最值解答题

阅读下面的例题：
解方程X2-∣X∣-2=0
解：（1）当x≥0时，原方程化为X2-X-2=0，解得X1=2，X2=-1（不合题意，舍去）.
（2）当X﹤0时，原方程化为X2+X-2=0，解得X1=1（不合题意，舍去），X2=-2.
∴原方程的根是X1=2，X2=-2.
请参照例题解方程X2-∣X-1∣-1=0.

已知关于x的方程，
（1）求证：此方程一定有两个不相等的实数根。
（2）若、是方程的两个实数根，且，求k的值

（1）探究下表中的奥秘，并完成填空：

一元二次方程	根	二次三项式
	________________
	_________________

（2）仿照上表把二次三项式（其中）进行分解？

解方程：

(12分) 阅读并解答问题
用配方法可以解一元二次方程，还可以用它来解决很多问题．例如：因为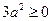，所以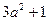就有最小值1，即，只有当时，才能得到这个式子的最小值1．同样，因为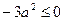，所以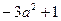有最大值1，即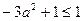，只有在时，才能得到这个式子的最大值1．

(1)当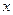=      时，代数式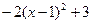有最      （填写大或小）值为          ．
(2)当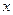=      时，代数式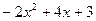有最      （填写大或小）值为         ．
(3)矩形花园的一面靠墙，另外三面的栅栏所围成的总长度是16m，当花园与墙相邻的边长为多少时，花园的面积最大？最大面积是多少?

(8分)
已知关于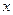的方程．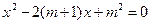
①当m取何值时方程有两个相等的实数根．
②为m选取一个适当的整数，使方程有两个不相等的实数根，并求出这两个实数根

用适当的方法解下列方程
⑴2（x＋2）2－8＝0                    ⑵
⑶3（x－5）2＝2（5－x）　　　　　　　　⑷x2＋5＝2x

（满分10分）解方程：
①                     ②

按要求解下列两个方程：
（1）（配方法）                （2）（公式法）