如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围。
如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点。 和
和 的顶点都在格点上。
的顶点都在格点上。
求证:

有这样一道题:“当 =0.302,
=0.302, =-0.239时,求(a+b)(a-b)+(4ab-8a2b2)÷4ab-a(a-2 b)多项式的值”,有一位同学指出题目中所给的条件“
=-0.239时,求(a+b)(a-b)+(4ab-8a2b2)÷4ab-a(a-2 b)多项式的值”,有一位同学指出题目中所给的条件“ =0.302,
=0.302, =-0.239”是多余的,问这位同学说的是否正确?若正确,请说明其理由;若不正确,多项式的值该是多少?
=-0.239”是多余的,问这位同学说的是否正确?若正确,请说明其理由;若不正确,多项式的值该是多少?
用边长为1cm的小正方形搭如下的塔状图形,则第n次所搭图形的周长是_ cm(用含n的代数式表示).

甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是
| A.①②③ | B.仅有①② | C.仅有①③ | D.仅有②③ |
在同一副扑克中抽出了16张牌,其中红心有x张,方块有2x张,其他均为梅花,现将这16张牌洗匀背面朝下放在桌面上,A同学任意抽1张,若为红心则A同学获胜,A同学把抽出的牌放回并洗匀背面朝下放在桌面上,B同学再任意抽1张,若为梅花,则B同学获胜.
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
如图,在直线 上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4= .
上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4= .
2010年广州亚运会吉祥物取名“乐羊羊”.图中各图是按照一定规律排列的羊的组图,图 有1只羊,图
有1只羊,图 有3只羊,……,则图⑩有( )只羊.
有3只羊,……,则图⑩有( )只羊. 
| A.53 | B.54 | C.55 | D.56 |
如图,小明从点A出发,沿直线前进20m后向左转300,再沿直线前进20m,又向左转300……照这样走下去,小明第一次回到出发点A,一共走了 __ 米。
(10分) 某通讯公司推出①、②两种手机通话月收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的月通话时间x(分钟)与收费y(元)之间的函数关系如图所示.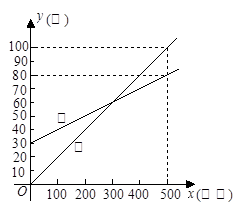
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户月通话时间的多少,给出经济实惠的选择建议
某校准备召开一次学生代表会,七(1)班有5个参会名额,其中男生必须有m人,于是七(1)班班主任确定从9名(5男4女,其中班长吴英为女生)候选人员中选取.若“选到吴英”的可能性是大于0但小于1,则m= .
古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图7中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
| A.13 =" 3+10" | B.25 =" 9+16" |
| C.36 =" 15+21" | D.49 = 18+31 |
将一些相同的小三角形按下图所示的规律摆放,请仔细观察,第 n个图形有 个小三角形.(用含 n 的代数式表示)